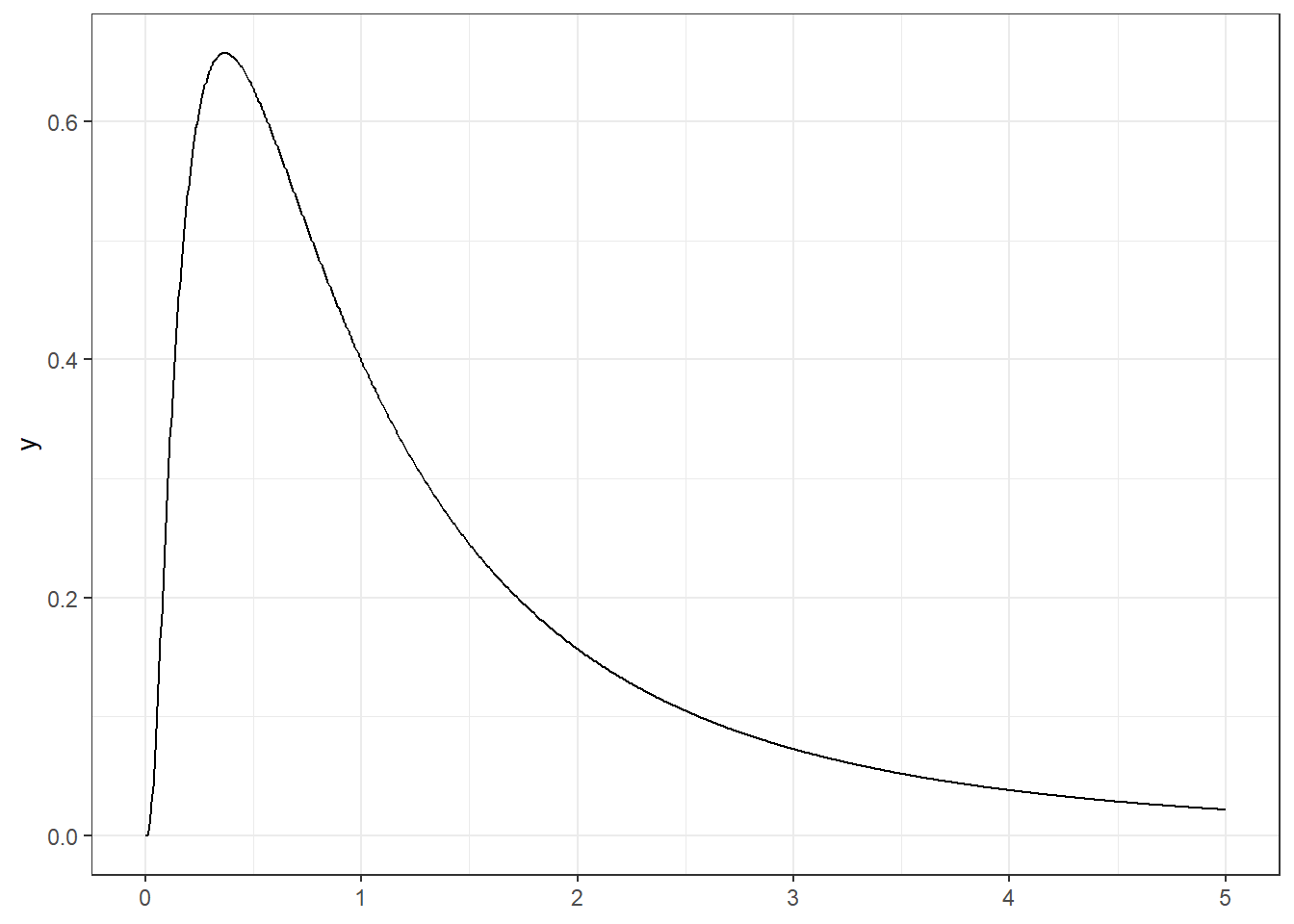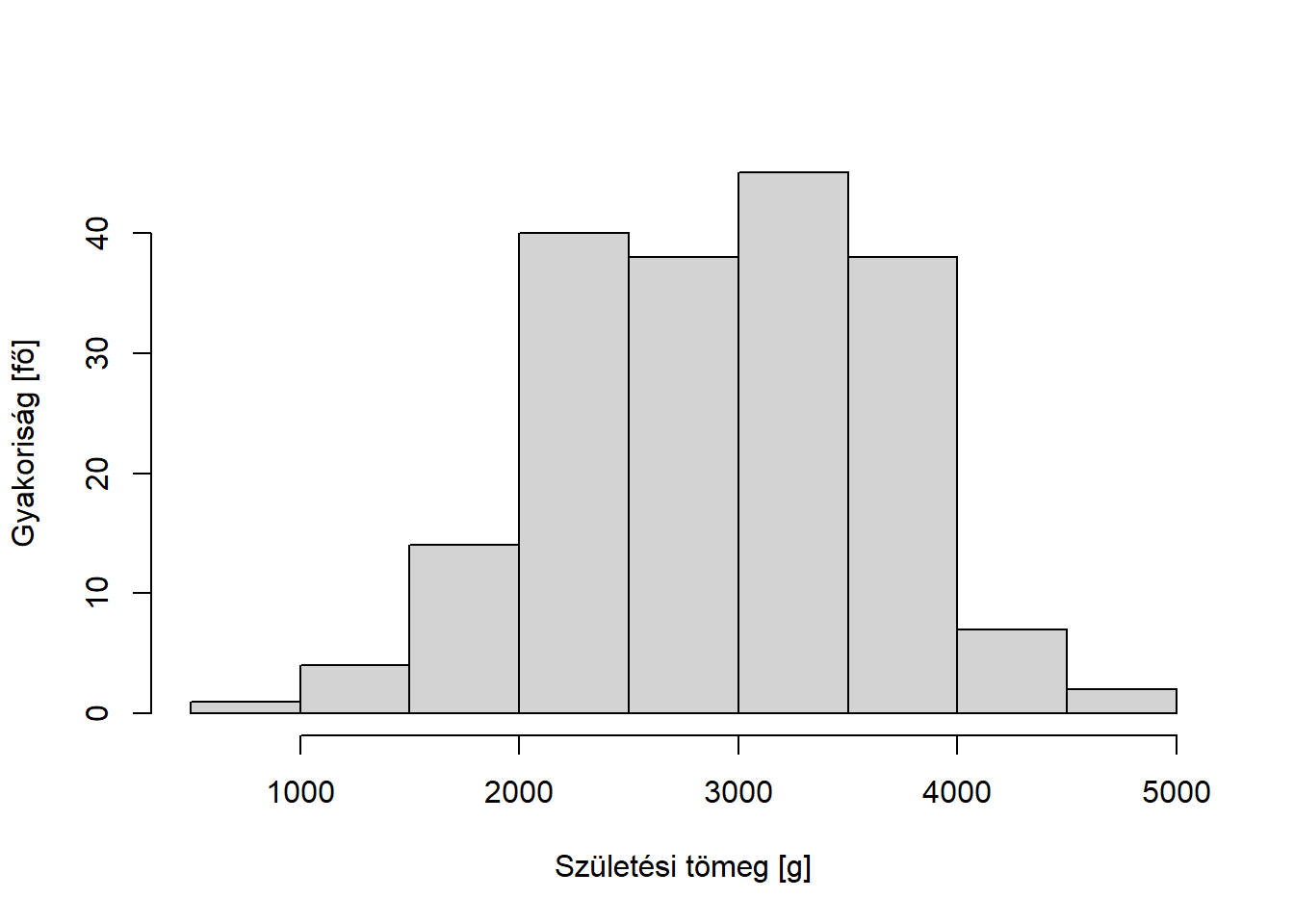A mutatószámok a megfigyelések valamilyen jellemzőjét próbálják meg egy-egy számba tömörítve megragadni. A következőkben aszerint csoportosítva mutatom be őket, hogy mi ez a megragadott jellemző.
Középértékek (centrális tendencia)
A középértékek egy nagyon érdekes állatfajt jelentenek: egyik oldalról ezek a leghétköznapibb mutatószámok, de valójában mégsincs igazán precíz definíciója annak, hogy mit értünk általában alattuk. Legtöbbször még a statisztika könyvek is inkább valamiféle verbális körülírással próbálkoznak, „mi körül csoportosulnak az értékek”, mi a „tipikus”, vagy „jellemző”, vagy „közepes” érték, de ez eléggé fából vaskarika, hiszen mégis mi a definíciója annak, hogy „jellemző” egy érték…? Ráadásul, mint az hamar ki fog derülni, ezek egy része még csak nem is igaz (pl. a megfigyeléseink fele 0, a másik fele 1000, akkor az 500-as átlag nemhogy nem tipikus vagy jellemző, de még csak elő sem fordul, sőt, még a környékén sincs megfigyelés). Az természetesen nagyon jó, ha az embernek van egy intuitív képe, amit a „közepes” magyar szó tényleg elég jól leír, de ezen túl nem hinném, hogy sokkal jobbat lehetne mondani, mint hogy a középérték az, amit a középérték-mutatók mérnek. És ezt egyáltalán nem viccből mondom, ennek a megfogalmazásnak fontos mondanivalója van: legyen az embernek intuitív képe, de ezen túl egész egyszerűen tudni kell, hogy pontosan mi a definíciója az adott mutatók, és az lesz a perdöntő.
Amikor azt mondtam, hogy leghétköznapibb, akkor nem csak azt értettem alatta, hogy közismert, hanem azt is, hogy bizonyos értelemben ez a legfontosabb mutatószám, jelesül, ha csak egyetlen számba kell sűrítenünk az egész eloszlást, akkor az tipikusan egy középérték. Ha több mutatót is közlünk egy eloszlásról, jellemzően akkor is a közép az, amit elsőként megadunk.
A legismertebb középérték a (számtani) átlag, jele \(\overline{x}\). Definíciószerűen nem más, mint az a szám, amivel helyettesítve minden megfigyelési egység értékét, az ún. értékösszeg, tehát a változó megfigyeléseinek összege változatlan maradna, vagyis, amire igaz, hogy \(\sum_{i=1}^n \overline{x} = n \cdot \overline{x} = \sum_{i=1}^n x_i\). Ebből már adódik, hogy az átlag:
\[\overline{x}=\frac{\sum_{i=1}^n x_i}{n}.\]
Úgy is mondhatnánk: ha egyenletesen szétosztanánk az értékösszeget minden megfigyelés között, akkor ennyi jutna mindenkire.
Azonnal látható, hogy ennek akkor van értelme, ha a különböző megfigyelések számtani összege valamilyen értelmes tartalommal bír. Ez kézenfekvően megvalósul akkor, ha olyanokról beszélünk, mint például egy cég dolgozóinak átlagfizetése, vagy egy ország bányáinak átlagos széntermelése: az összeg itt az, hogy mennyi bért fizet ki a cég, vagy mennyi szenet termel az ország, ezek mind teljesen értelmes, tárgyterületi tartalommal, jelentéssel bíró számok. Érdekesebb a kérdés akkor, ha mondjuk egy osztály átlagos testtömegéről beszélünk, de kis ráolvasással ez is megindokolható (az összeg az, hogy mennyit mutatna a mérleg, ha együtt állna rá mindenki).
Amikor viszont biztosan nem alkalmas mutató az átlag, az az eset, ha az összegnek egyáltalán nincs értelme. Tipikus példa erre az, ha a változó valamilyen növekedési ütemet jelent időben: ha egy alany testtömege egy évben 1,2-szeresére nőtt, rákövetkező évben pedig 1,3-szeresére, akkor az össznövekedés nyilván nem a növekedések összege (\(1,\!2 + 1,\!2 = 2,\!4\)), hanem azok szorzata (\(1,\!2 \cdot 1,\!2 = 1,\!44\)) lesz. Ebben az esetben, tehát, ha nem az összeg, hanem a szorzat értelmes, a mértani átlag fogalmához jutunk el (az a szám, amivel a megfigyelések szorzata – nem összege – ugyanaz maradna).
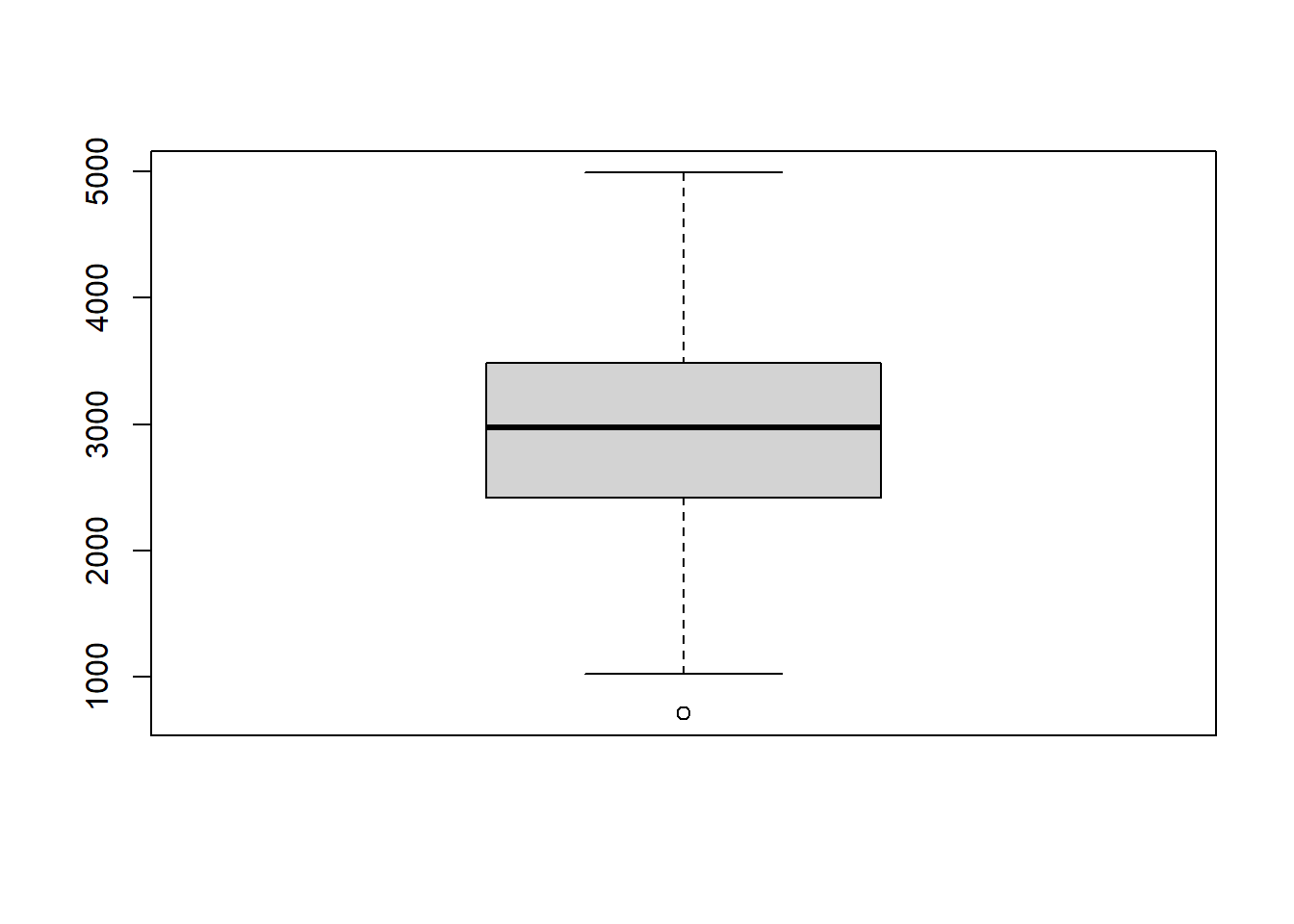
A születési tömegek átlaga 2944.5873016 gramm. Meglehetősen erőltetett azt mondani (noha formailag természetesen helyes), hogy ez azt jelenti, hogy az adatbázisban szereplő újszülöttek össz-testtömege akkor maradna változatlan, ha mindegyikük 2944.5873016 gramm lenne; talán jobb, ha egyszerűen azt mondjuk, hogy ez egy középmutatója a csecsemők születési tömegei eloszlásának.
Az átlagnak két további nevezetes tulajdonsága említést érdemel. Az egyik, hogy a megfigyelések tőle vett eltéréseinek az összege zérus; ez könnyen belátható:
\[\sum_{i=1}^n \left(x_i - \overline{x}\right) = \sum_{i=1}^n x_i - \sum_{i=1}^n \overline{x} = n\overline{x} - n\overline{x} = 0.\]
A másik fontos tulajdonsága, hogy az összes szám közül ez az, amire igaz, hogy a megfigyelések tőle vett eltérésnégyzeteinek az összege minimális, tehát a \(\sum_{i=1}^n \left(x_i - c\right)^2\) kifejezés akkor minimális, ha \(c = \overline{x}\). Fontos megjegyezni: a négyzetre emelés eltünteti az előjelet, vagyis az eltérésnégyzet, szemben az előbbi előjeles eltéréssel, egyfajta távolság – ilyen értelemben ez a megállapításunk azt mondja, hogy az átlag van a legközelebb a pontokhoz, ha ugyanannyira számít minden ponthoz a közelség! Ez egyfajta alátámasztását adja az átlag középérték jellegének. (Az összefüggés egyértelmű, ez a minimum-tulajdonság nem csak igaz az átlagra, de az átlag az egyetlen szám, amire igaz, tehát elvileg akár így is bevezethettük volna az átlagot, az értékösszeg egyenletes szétosztása helyett.)
Az átlag előnye, hogy mindenki számára közismert, kényelmesen kezelhető, bevett mutató. (Ez olyannyira erős tényező, hogy nagyon sok orvosi publikáció még akkor is erőlteti az átlag használatát, amikor az – a mindjárt részletezendő okokból – nem célszerű.)
Az átlag legnagyobb hátránya, hogy nem robusztus. A gyakorlatban ez két módon szokott megjelenni (matematikailag természetesen ugyanaz van a hátterében, ez ugyanazon jelenség két megjelenési formája, csak parktikus szempontokból érdemes különválasztani).
Az egyik probléma az outlierek ügye: így szokás hívni a csoportosulás alaptendenciájától jelentősen eltérő értéket vagy értékeket. Ez megint kettéoszlik jellegét tekintve: egyfelől előfordulhat, hogy az adatokat valamilyen eltérő mechanizmus generálta (például az alapvetően egészségesekből álló mintába bekerül néhány beteg is, akiknek a vizsgált laborváltozója lényegesen magasabb), másfelől idetartoznak az adatbeviteli hibák is. Akármelyikkel is állunk szemben, az átlag elveszíti szokásos tartalmát. Vegyük mondjuk az utóbbi példát: van 1000 újszülöttünk, és egyetlen egynél – de csak egynél – elrontjuk az adatbevitelt, mondjuk 3 kg helyett 3 tonnát írunk be a súlyaként. Ekkor (hiába is korrekt az adatok 99,9%-a!) az átlag teljesen értelmetlenné válik: az átlagos születési tömeg 6 kg lesz… (ha egyébként mindenki 3 kg körüli). Ezért nem robusztus az átlag: hiába volt az adatok abszolút túlnyomó többsége korrekt, minödssze egyetlen egy hiba elég volt ahhoz, hogy az átlag értelmetlenné váljon.
Az outlierek esetén két kérdés merül fel: a detekció, tehát annak azonosítása, hogy egy megfigyelés outlier (mi ennek a kritériuma?), valamint a kezelés. A fenti adathibás példa azt sugallja, hogy a „kezelés” az egyszerűen az ilyen megfigyelések törlése, és ha valóban elírás van a hátterében, úgy, hogy a valódi értéket már nem tudjuk kideríteni, akkor tényleg nem tehetünk sokkal jobbat. Ez azonban szükségessé teszi a megfelelő detekciót, így annak is lehet értelme, hogy e helyett inkább olyan statisztikai módszereket használjunk, amelyek robusztusak, azaz nem érzékenyek az outlier-ek jelenlétére (tehát például, mint láttuk, nem átlagot…), hiszen így nem kell – potenciálisan hibával terhelt módon – azonosítanunk, hogy egyáltalán mi az outlier, megspóroljuk ezt a definíciós problémát. Végezetül annak is lehet értelme, hogy a fentiekkel szemben ne – valamilyen módon – megszabadulni akarjunk az outlier-ektől, hanem ellenkezőleg, kimondottan megragadjuk ezeket, és egy finomított statisztikai megközelítés segítségével explicite modellezzük őket is (például az egészséges-beteg laborváltozós esetben külön eloszlást illesszünk az egészségesekre és a betegekre).
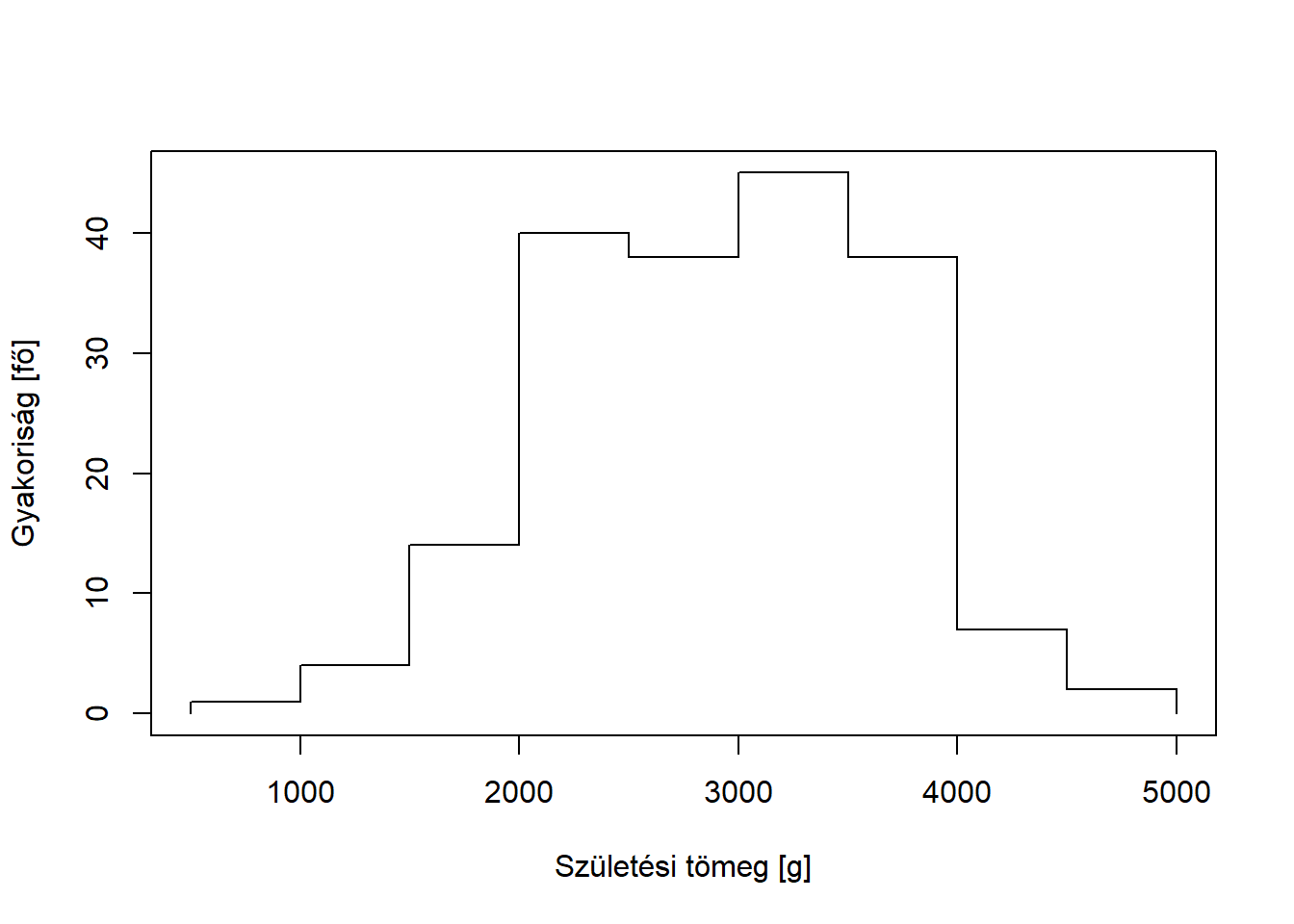
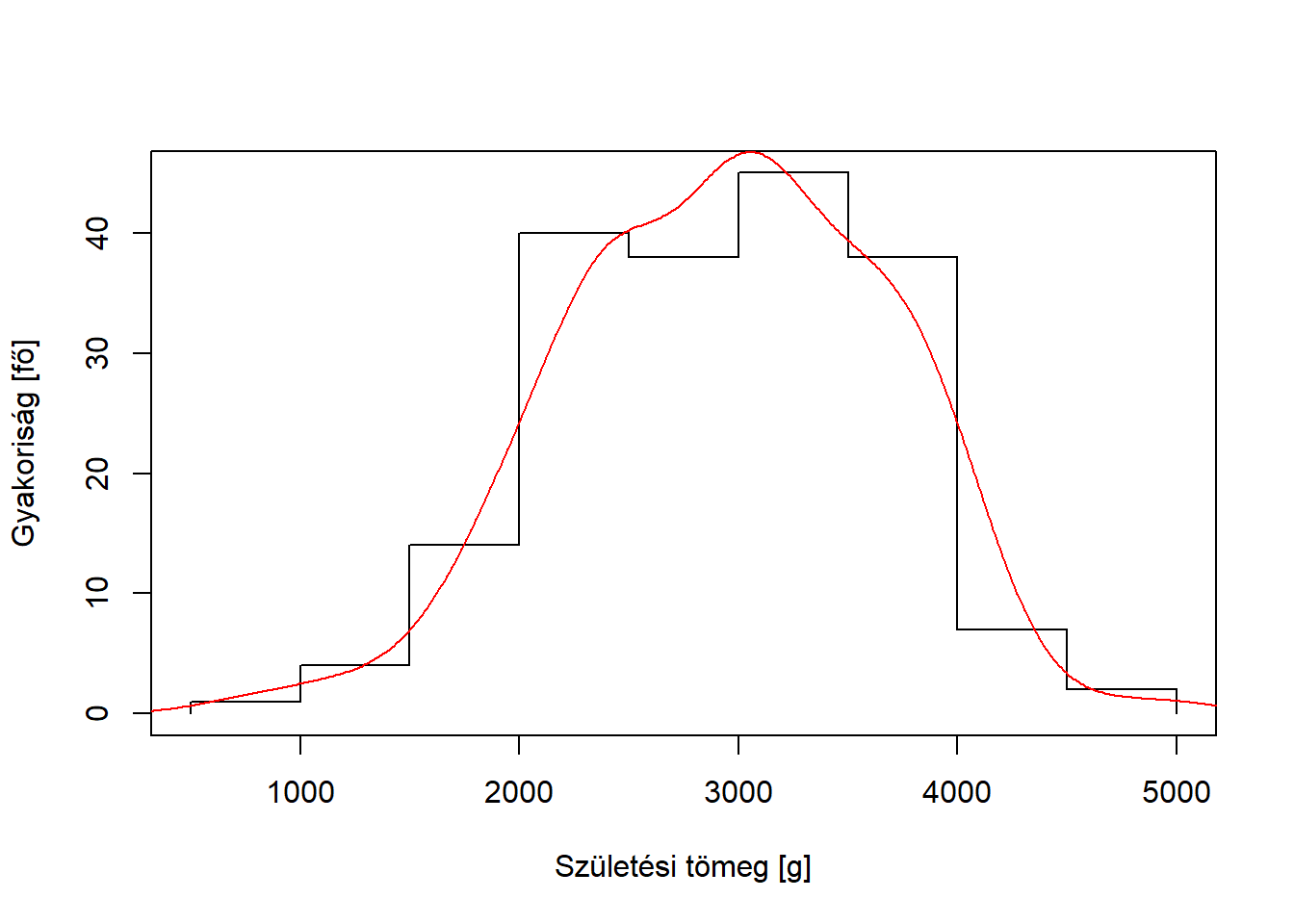
A robusztusság azonban nem csak az outlierek kapcsán érdekes, sőt, a gyakorlatban nagyon fontos tud lenni akkor is, ha egy fia outlier nincs, semmilyen adatbeviteli hiba nem történt, semmilyen többitől eltérő csoportosulási tendencia nem lép fel. Mikor? Az úgynevezett ferde eloszlások esetén. A ferdeség azt jelenti, hogy az eloszlás aszimmetrikus: egyik irányban messzebre szóródik, mint a másikban. Erre orvosi példákat könnyű mondani, vegyünk egy olyan laborváltozót mint a CRP: ez egy gyulladásmarker, koncentrációja normálisan néhány mg/dl a vérben, csakhogy – és most jön a lényeg – lefelé nem tud szabadon szóródni, hiszen valaminek a koncentrációja, így negatív nem lehet. Felfelé azonban tud, hiszen ilyen felső korlát nincs, nyugodtan lehet 10, 50, 100, vagy akár annál is több az értéke. Lényegében arról van szó, hogy 0-nál egy „fal” van, ami megakadályozza a szóródást, de a kulcs, hogy ez csak egy egyik irányban történik meg – ez hozza létre a ferdeséget. Illusztratív példát mutat ilyen eloszlásra a 2.2. ábra.
Mi fog történni, ha ilyen változónak számítjuk az átlagát? Az ábrán szereplő példában ez 1,6 körül lesz, ami csak azért „furcsa”, mert első ránézésre meglepően magas: úgy érzi az ember, hogy valamiért egészen az eloszlás jobb széle felé van, egyáltalán nem a közepénél (ahol lennie „kellene”, ha már egyszer középmutató). Ez bizonyos értelemben jogos, hogy számszerűsítsük a dolog: a megfigyelések nagyjából 69%-a lesz kisebb az 1,6-nél! Na de hogy lehet 1,6 az átlag, ha egyszer a megfigyelések több mint kétharmada kisebb nála?! – kérdezhetné valaki. A válasz az, hogy nagyon könnyen: az eloszlás jobb szélén ugyan ritkán vannak megfigyelések, de azok értéke lényegesen nagyobb, mint a többi, ami fel fogja húzni az átlagot ugyanis – és most jön a lényeg! – a másik oldalról nem lesz, még kis számban sem, olyan érték, ami a túl oldalra kilógva tudná ezt ellensúlyozni! Ez egyáltalán nem outlier-probléma a fenti értelemben, mégis, az átlag használata megkérdőjeleződik.
Nagyon fontos hangsúlyozni, hogy ez a jelenség nem azt jelenti, hogy az átlag „elromlott” ezekben az esetekben. Az átlag tényleg annyi (ezen belül is különösen: tényleg 6 kg kell legyen mindenki születési tömege, hogy kiadja az összeget, amiben 3 tonna is van, tényleg 1,6 kell legyen mindenki CRP-je, hogy kiadja az összeget, amiben a kis számú nagy érték is benne van). Az átlag nem „rossz” ilyenkor, maximum nem felel meg annak, hogy mi a szubjektív képünk arról, hogy „közép”! De ez nem az átlag hibája; legfeljebb más mutatóra van szükségünk, ami jobban egybevág a szubjektív képünkkel. (Itt is előjön, amit a felvezetőben mondtam: lehet verbális körülírásokkal élni, de egy ponton túl csak az lesz a perdöntő, hogy mi a definíció.)
Vannak bizonyos ad hoc javítások erre a robusztussági problémára, talán egyet érdemes itt megemlíteni, a trimmelt (vagy nyesett) átlagot: ezt úgy kapjuk, hogy elhagyjuk a legkisebb és legnagyobb adott számú elemet, és csak a maradékot átlagoljuk ki. Tipikusan az elhagyott megfigyelések száma alul és felül is a mintanagyság 2,5%-a; ebben az esetben 5%-os trimmelt átlagról beszélünk. (Bár elsőre ez szokatlan mutatónak tűnhet, és a tudományos irodalomban tényleg ritkábban is használják, de számos pontozásos sportágban épp ilyen elven alakítják ki a zsűri „átlagos” pontszámát.) A születési tömegek 5%-os trimmelt átlaga 2957.4152047 gramm, ami egyúttal azt is mutatja, lévén, hogy közel van a szokásos átlaghoz, hogy a születési tömegek aránylag szimmetrikus eloszlásúak, vélhetően komoly outlier nélkül.
Alapvetően más megközelítését jelenti a centrális tendencia megragadásának a medián használata, melynek jele \(\mathrm{Me}_x\). A medián nem más, mint a nagyság szerint sorbarendezett megfigyelések közül a középső. (Amennyiben a mintanagyság páros, úgy nyilván két „középső” is van, ez esetben megállapodás kérdése, hogy mit nevezünk mediánnak; vehetjük például a kettő átlagát.) Úgy is mondhatjuk, hogy a medián a felezőpont, az az érték, amiről elmondható, hogy alatta és felette is a mintaelemek fele található.
A medián szintén a centrális tendenciát jellemzi, csak épp kevésbé megszokott módon, mint az átlag – ez egyúttal használatának egyik fő gátja is: sok ember számára a medián tartalma (és egyáltalán, értelme) kevésbé ismert, így e mutató nem annyira jól kezelhető. Előnye viszont a robusztusság, ilyen szempontból az átlaggal szemben a másik végpontot képviseli: míg az átlag extrém érzékeny volt, addig a medián extrém robusztus. Ez mind az outlier-es esetekben, mind a ferde eloszlásoknál érvényesül. A minta minden medián feletti értéke (az egyszerűség kedvéért most gondoljunk páratlan mintanagyságra) tetszőlegesen megnövelhető (akár az összes egyszerre is), vagy a medián alatti értékek tetszőlegesen lecsökkenthetőek (akár az összes egyszerre is), vagy akár a kettő együtt is, a medián értéke nem változik! Az előző példánkban: hiába a 3 tonnás csecsemő, a medián marad értelmes, 3 kg körüli, a CRP esetében pedig 1 lesz a medián – nézzünk vissza az ábrára (2.2. ábra) ez valóban sokak érzete szerint közelebb van a „középhez”, mint az 1,6-os átlag.
A medián hátránya (azon túl, hogy más az értelmezése, tartalma, de ez nem hátrány, csak egy jellemző), hogy a jó robusztusságért cserében kevesebb információt használ fel a mintából; ezt épp a mintaértékek meglehetősen szabad „állítgathatósága” mutatja. Hogy ez miért baj, az precízen csak induktív statisztikai keretben lehet megérteni, az ottani tárgyalás után már érthető lesz, hogy mit jelent az, hogy a medián kevésbé hatásos becslő mint az átlag.
A tanulság összességében az, hogy ha előre tudható, hogy a háttéreloszlás szimmetrikus-közeli, akkor érdemes átlagot használni, ha nem, vagy outlier-ek jelenlétére is fel kell készülni, akkor jobb a medián ilyen szempontból. Az is gyakori megoldás – és ugyan az áttekinthetőségből feláldoz valamennyit, de cserében bombabiztos – ha egész egyszerűen közöljük mindkettőt.
Érdemes röviden megemlíteni, hogy a mediánnak is van távolság-optimum jellegű tulajdonsága, ráadásul egészen hasonló az átlagéhoz. Emlékeztetőül: az átlag az a szám, amire igaz, hogy a megfigyelések tőle vett távolságainak az összege minimális, ha a távolság alatt a különbség négyzetét értjük. Nos, a mediánra betű szerint ugyanez igaz, csak távolság alatt nem az eltérés négyzetét, hanem abszolútértékét kell érteni! A \(\sum_{i=1}^n \left| x_i - c \right|\) akkor minimális (és csak akkor), ha a \(c\) a medián. Itt is elmondható ebből fakadóan, hogy ez újabb alátámasztását adja a medián középérték jellegének.
A születési tömegek mediánja 2977 gramm, azaz a 2977 gramm az a testtömeg, amiről elmondható, hogy az újszülöttek fele kisebb ennél, fele nagyobb. (Láthatóan közel van az átlaghoz, újból megerősítve, hogy ez valószínűleg egy szimmetrikus eloszlás, nagy outlier-ek nélkül.)
Ahogy a medián a minta „felezőpontja”, ugyanúgy definiálhatók általános osztópontok; ezeket kvantiliseknek nevezzük. A \(p\)-kvantilis (\(0<p<1\)) az az érték, amiről elmondható, hogy a megfigyelések \(p\)-ed része kisebb nála, \(\left(1-p\right)\)-ed része nagyobb nála. (Tehát a medián az \(1/2\)-kvantilis.) Gyakorlati szempontból nagyobb jelentősége van még a negyedelőpontoknak, melyek neve kvartilis. Ilyenből tehát három van: a \(p=1/4,2/4=1/2,3/4\)-kvantilis, ezek közül a középső persze ugyanaz mint a medián. A másik kettőt alsó és felső kvartilisnek szokták nevezni, és \(Q_1\)-gyel, illetve \(Q_3\)-mal jelölik. Tehát például \(Q_1\) az a szám, amire igaz, hogy a minta egynegyede nála kisebb értékű, háromnegyede nála nagyobb. Ezek valójában már nem is a centrális tendenciát, hanem általában az eloszlás alakját mutatják, mégpedig robusztus módon (ugyanazon okból, mint amiért a medián is robusztus). Ritkábban, de szokták használni ugyanerre a célra a tizedelőpontokat, nevük decilis (\(D_1,D_2,\ldots,D_9\)) és a századolópontokat, nevük percentilis (\(P_1,P_2,\ldots,P_{99}\)). A 90. percentilist például gyakran használják olyankor, ha az eloszlás széli viselkedésének jellemzésére van szükség – mi a legrosszabb eshetőség? – amit első ránézésre a maximum mutatna, csak a 90. percentilis sokkal robusztusabb: a maximum nagyon ingadozó, olyan értelemben, hogy egyetlen érték is odébbhúzza (az nagyon esetleges lehet, hogy pont a legnagyobb mennyi); a 90. percentilis viszont továbbra is az eloszlás szélét méri, de kevéssé ingadozó, sokkal robusztusabb módon.
A korábbi értelemben vett módusz használatának a folytonosság miatt általában nincs értelme mennyiségi változó esetén, hiszen még az is lehet, hogy minden konkrét értékből csak egyetlen egy fordul elő, ahogy arról már volt is szó. Folytonos változó esetén emiatt a módusz többé nem a leggyakoribb kimenet, hanem a sűrűségfüggvény maximumhelye – csakhogy sűrűségfüggvényünk nincsen, azt legfeljebb közelíteni tudjuk a mintából, valamilyen simítóeljárással (részletesebb lásd a grafikus módszerek között, a 2.4.2. pontban). Ez lehet egy sima osztályközös gyakorisági sor / hisztogram (az is egyfajta simítás!), ez esetben modális osztályközről szokás beszélni, mint a legnagyobb gyakoriságú osztályköz / a hisztogram legmagasabb oszlopa, de használhatunk simításra magfüggvényes sűrűségbecslőt is (2.4.2.3. pont), ez esetben a maximum egyetlen pont lesz. Ez azonban még deskriptív statisztikai értelemben is csak egy közelítés. Az ilyen módon vett módusz használata ritka a mindennapi biostatisztikai gyakorlatban.
Ennek kapcsán még annyit megjegyzek, hogy átlagot, mediánt (és általában minden egyéb mutatószámot is) lehetséges osztályközös gyakorisági sorból, a nyers mintaelemek ismerete nélkül is számolni, persze ekkor már csak közelítő jelleggel.
Szóródás
Szóródásnak nevezzük azt, hogy a megfigyelések milyen szorosan csoportosulnak azon érték körül, ami körül csoportosulnak (lásd a centrális tendenciát!), más szóval mennyire ingadoznak a megfigyelések, mekkora változékonyság van bennük. A gyakorlatban ez a második legfontosabb kérdés: ha csak egy jellemzőt adhatunk meg, akkor az a centrális tendencia lesz, de ha kettőt, akkor megadjuk azt is, hogy mekkora a szóródás.
A minta szóródásának legegyszerűbb mérőszáma a legkisebb (\(\mathrm{Min}\)) és a legnagyobb (\(\mathrm{Max}\)) mintaelem értéke, a mintaminimum és mintamaximum, illetve kettejük különbsége, melyet terjedelemnek nevezünk és gyakran \(R\)-rel jelölünk: \(R=\mathrm{Max}-\mathrm{Min}\). Ezek előnye, hogy teljesen egyértelmű a tartalmuk, hátrányuk, hogy rendkívül érzékenyek arra, hogy konkrétan milyen mintát vettünk a sokaságból, ezért, bár gyakran megadják információ gyanánt, a szóródás számszerű jellemzésére ritkán használják.
A születési tömegek mintaminimuma 709 gramm, mintamaximuma 4990 gramm, így e változó terjedelme 4281gramm.
Az egyik alapvető mutatója a szóródásnak a szóránégyzet (vagy variancia), jele általában \(s_x^2\). A szórásnégyzet tulajdonképpen a legkézenfekvőbb jellemzője a szóródásnak, hiszen nem más, mint a átlagtól vett átlagos eltérés. Az egyetlen amire vigyázni kell, hogy az eltérés alatt mit értünk: ha egyszerűen a megfigyelés és az átlag különbségét vennénk, az nem lenne jó, mert a pozitív és a negatív eltérések csökkentenék (sőt, belátható, hogy kioltanák) egymás hatását. Ezért inkább négyzetre emeljük ezt a különbséget, hogy megszabaduljunk az előjeltől, hogy a \(+1\) és a \(-1\) eltérés hatása ugyanolyan legyen, és ezzel már jók vagyunk:
\[s_x^2=\frac{\sum_{i=1}^n \left(x_i-\overline{x}\right)^2}{n}.\]
A szórásnégyzet problémája, hogy a mértékegysége nem ugyanaz, mint az eredeti változóé (a négyzetremelés miatt). Ha szeretnénk a szóródást ugyanazon a skálán jellemezni, akkor egy gyökvonással visszatérhetünk; ezt a mutatót hívjuk szórásnak, jele \(s_x\):
\[s_x=\sqrt{s_x^2} = \sqrt{\frac{\sum_{i=1}^n \left(x_i-\overline{x}\right)^2}{n}}.\]
(A kettő neve nem keverendő: a „szóródás” a jellemző, a „szórás” egy lehetséges mutatószáma ennek a jellemzőnek.)
Deskriptív esetben néha inkább mintavarianciát, illetve mintaszórást mondanak (hogy a megfelelő sokasági jellemzőtől megkülönböztessék – sajnos nincs akkora szerencsénk, mint az átlagnál, ahol az „átlag” és a „várható érték” révén két teljesen különböző szavunk van a mintabeli, tehát statisztikai és a sokasági, tehát valószínűségszámításos fogalomra).
A fent definiált mutatót szokás precízen korrigálatlan mintavarianciának, illetve mintaszórásnak nevezni, ezzel szemben a korrigált mutatóban nem \(n\)-nel, hanem \(n-1\)-gyel osztunk le. Például a korrigált mintaszórás, jele \(s_x^{\ast}\):
\[s_x^{\ast}=\sqrt{\frac{\sum_{i=1}^n \left(x_i-\overline{x}\right)^2}{n-1}}.\]
A különbségük oka csak a következtető statisztikában válik világossá.
A születési tömegek korrigált mintaszórása 729.2142952 gramm, tehát az újszülöttek testtömegeinek átlaguk körül vett ingadozásának átlaga 729.2142952 gramm.
A szórás hátránya, hogy – az átlaghoz hasonlóan – nem robusztus mutató. (Egyrészt azért nem, mert az átlagtól vett eltérések nézi, ami eleve nem robusztus középmutató, másrészt ezeket átlagolja, ami ugyebár nem robusztus, ráadásul a négyzetreemelés még ki is emeli a különbségeket.) Egyik gyakran alkalmazott robusztus alternatíva az interkvartilis terjedelem (jele \(IQR\)), ami a felső és az alsó kvartilis különbsége:
\[IQR=Q_3-Q_1.\]
Mondhatjuk azt is, hogy az IQR az adatok középső 50%-ának szélessége.
Az interkvartilis terjedelem a robusztus kvartiliseken alapul, így robusztus mutató, és könnyen látható, hogy tartalmilag a szóródást jellemzi, hiszen minél jobban szóródott az eloszlás, annál távolabb lesz az alsó és a felső negyedelőpontja.
A születési tömegek interkvartilis terjedelme 1073 gramm, tehát az a tömeg, ami fölött az újszülöttek egynegyede (és alatta háromnegyede) van, 1073 grammal nagyobb annál a tömegnél, ami fölött az újszülöttek háromnegyede (és alatta egynegyede) van, tehát 1073 gramm szélességben szóródik a születési tömegek középső 50%-a.
Egy másik lehetőség a szórás „megjavítása”, olyan módon, hogy kiküszöböljük a nem-robusztusság fent említett forrásait: az eltéréseknek nem a négyzetét, hanem az abszolút értékét vesszük, az eltéréseket nem az átlagtól hanem a mediántól vesszük, végül pedig nem is átlagoljuk őket, hanem a mediánjukat képezzük. Az így kapott mutató neve medián abszolút eltérés, jele \(MAD\), tehát
\[MAD=\mathrm{Me}\left(\left|x_i-\mathrm{Me}\left(x\right)\right|\right).\]
(A szakirodalom itt nem teljesen egyértelmű: néha \(MAD\)-nak nevezik azt a mutatót is, ahol csak az első javítást csinálják meg, tehát abszolútértéket vesznek, de azokat továbbra is csak átlagolják, és az eltéréseket is az átlagtól veszik.)
A születési tömegek medián abszolút eltérése 563 gramm, tehát az újszülöttek testtömegeinek mediánjuk körül vett (abszolút) ingadozásának mediánja 563 gramm.