data(birthwt, package = "MASS")
birthwt$race <- factor(birthwt$race, levels = 1:3,
labels = c("Kaukázusi", "Afro-amerikai", "Egyéb"))
birthwt$smoke <- factor(birthwt$smoke, levels = 0:1,
labels = c("Nem dohányzó", "Dohányzó"))4 Haladó adatvizualizáció
A deskriptív statisztika kapcsán (2. fejezet) lépten-nyomon láttunk adatvizualizációkat. Még csoportosítási szempont is volt, úgy hívtam ott az ilyeneket, hogy a deskriptív statisztika grafikus eszközei. Annyiban azonban korlátozott volt az adatvizualizáció ottani tárgyalása, hogy kizárólag az R beépített1 lehetőségeit használtuk; ezt úgy is szokták hívni, hogy base R grafika.
Ebben a fejezetben elsőként (4.1. alfejezet) jobban kontextusba helyezzük a base R grafikát: mi az egyáltalán, milyen előnyei és milyen korlátai vannak? Erre már csak azért is szükség van, mert korábban, a deskriptív statisztikáról szóló fejezetben ezeket az eszközöket magától értetődőnek vettem, anélkül, hogy jobban vizsgáltuk volna az előnyeit és hátrányait. A korlátok miatt több, tudományos adatvizulizációra kifejezetten alkalmas haladó adatvizualizációs csomag is kialakult az évtizedek alatt – mi is megismerkedünk ezt követően az egyik ilyen csomaggal, a ggplot2-vel (4.2. alfejezet). Elsőként megismerjük az általános működését, és megnézzük a korábban már látott, base R grafikás – elemi – vizualizációk ggplot2 alatti megvalósítását is. Ha ez megvan, akkor továbbléphetünk a fejezet fő céljára: meg fogunk ismerkedni a többváltozós vizualizációkkal, különösen hangsúllyal kitérve a vizualizáció stratégiai kérdéseire, tehát immár elszakadva a technikai megvalósítástól, arra fogunk fókuszálni, hogy adott tudományos kérdéshez mi lesz a legcélszerűbb ábra, hogyan tudjuk megtervezni úgy a vizualizációt, hogy legjobban segítse a kérdés megválaszolását.
4.1 A base R grafika és korlátai
A deskriptív statisztikánál (2. fejezet) mindenhol base R grafikát használtam az adatvizualizációk elkészítésére, így az ottani kódok és ábrák áttekintése már jó képet ad e vizualizációs rendszer főbb jellemzőiről. A base R grafikában minden ábratípushoz egy saját függvény tartozik, és az ábra testreszabását a függvény argumentumainak beállításával tudjuk végezni. (Az argumentumok meglehetősen konzisztensek base R grafikán belül, tehát ha valahol megtanultuk, hogy a main argumentummal lehet címet adni az ábrának, akkor jó eséllyel számíthatunk arra, hogy ez minden base R grafikás ábránál így lesz.) Base R grafikával jellemzően elemi ábrákat lehet legyártani, azaz olyanokat, amik egyszerűbb esetekre önmagukban is megoldást jelentenek, a bonyolultabbakat pedig nagyon gyakran ezekből, mint építőkövekből kell összerakni (vagy több kombinálásával, vagy egynek valamilyen variálásával). Mindazonáltal ehhez az építkezéshez az base R grafika már jellemzően kevés segítséget ad.
A base R grafika megtanulása, korlátaival együtt is, hasznos. Egyrészt, mert egyszerű, és abban a fejezetben a hangsúly sokszor az elméleti kérdéseken volt, így jól jött, hogy az R-es kivitelezés nem vonta el a figyelmet, gyorsan, könnyen megírható, magától értetődő kódokat lehetett használni. Ez nem csak didaktikai kérdés: a valós napi gyakorlatban is sokszor előfordul, hogy valami egyszerű ábrára kell villámgyorsan rápillantani, amit csak „belső használatra” gyártana le az ember; ilyenkor sokszor az egyébként haladó grafikát használók is inkább csak gyorsan a base R grafikához nyúlnak. Úgyhogy hasznos, ha az ember ezt is ismeri (túl azon, hogy az alapokat „illendő” ismerni). Mindemellett, a base R grafikának előnyei is vannak, például jól támogatja azt, ha egy meglevő ábrára akarunk rárajzolni valamit.
Ezzel együtt is, a base R grafikának komoly limitáció vannak. Az egyik az esztétika: sokan azt mondják, hogy a base R grafikás ábrák nem néznek ki túl jól. Ez persze elég szubjektív (mi az, hogy „jól néz ki” egy ábra?), de ami objektív, hogy base R grafikában az elemi ábrák ugyan könnyen megvannak, de ha komplexebb ábrákat akarunk összerakni, akkor nagyon hamar jönnek a gondok. Egy ponton túl ezeket egész egyszerűen nem is lehet megvalósítani base R grafikában, de ha meg is lehet, az is sokszor macerás, időigényes, sok kódolást igényel. De, ami sokkal fontosabb, hogy ez nem csak idő és energia kérdése: a még nagyobb baj, hogy a sok macera mind-mind hibalehetőség. Nézzünk is meg pár példát erre!
Alanyunk a megszokott adatbázis lesz:
A feladat pedig legyen a következő: vizualizáljuk a születési tömegek eloszlását rassz szerint! Azt is mondhattam volna: vizualizáljuk a születési tömegek és a rassz kapcsolatát; de az előbbi megfogalmazás már a megoldást is sugallja: kell egy eszköz mennyiségi változó vizualizálására (amit használnánk ha csak simán a születési tömegek eloszlását akarnánk ábrázolni, mondjuk egy hisztogram vagy magfüggvényes becslő), majd ezt kell alkalmazni, csak most nem egyszer, hanem többször – minden rasszra külön-külön. Ezeket az ábrákat utána persze megfelelően ki is kell rajzolni. (Ha valaki szeretné a dolgot a deskriptív statisztikáról szóló fejezet tipológiájába beilleszteni: ez lényegében egy kétváltozós kapcsolat vizualizálása volt, ahol az egyik változó minőségi, a másik mennyiségi!)
Válasszuk mondjuk először eszközként a hisztogramot! Ekkor tehát több hisztogramot kell legyártanunk, majd valahogy ábrázolnunk. Az utóbbi kapcsán belefutunk a hisztogramok egyik problémájába: nem lehet őket egymásra plottolni, például különböző színekkel megkülönböztetve (pedig az lenne az ideális – erről később még sok szó lesz), ezért csak egymás mellé lehet őket plottolni. Ami nem annyira jó, illetve azt a kérdést is felveti, hogy egymás alá vagy egymás mellé plottoljuk? Erről később még fogunk beszélni, most maradjunk abban, hogy egymás alá plottolunk. Base R grafikában ezt a feladat csak úgy tudjuk megoldani, hogy a plottolási felületet kézzel szétosztjuk több, kisebb részfelületre – erre szolgál az mfrow nevű opció. Ha ezt beállítjuk, akkor az első kiplottolt ábra a bal felső kis részfelületre kerül, és minden további ábra, ha kiadunk valamilyen plottolási utasítást, a következőre (ha elérünk az utolsóig, akkor kezdődik a dolog elölről a bal felső résznél, felülírva az ábrákat).
Nekünk tehát most három sorra (és egy oszlopra, hiszen oszlopokat nem akarunk) kell osztanunk a felületet. Illetve bocsánat, általában véve nem tudhatjuk, hogy mennyire lesz szükségünk, úgyhogy először ezt ki kell derítenünk:
length(unique(birthwt$race))[1] 3Ha ez megvan, akkor a par(mfrow = c(3, 1)) paranccsal végrehathatjuk a szétosztást (a par parancs szolgál a grafikus paraméterek beállítására). Ezt követően kirajzolhatjuk2 a hisztogramokat:
par(mfrow = c(3, 1))
par(mar = c(5.1, 4.1, 2.1, 2.1))
hist(birthwt[birthwt$race == "Kaukázusi",]$bwt)
hist(birthwt[birthwt$race == "Afro-amerikai",]$bwt)
hist(birthwt[birthwt$race == "Egyéb",]$bwt)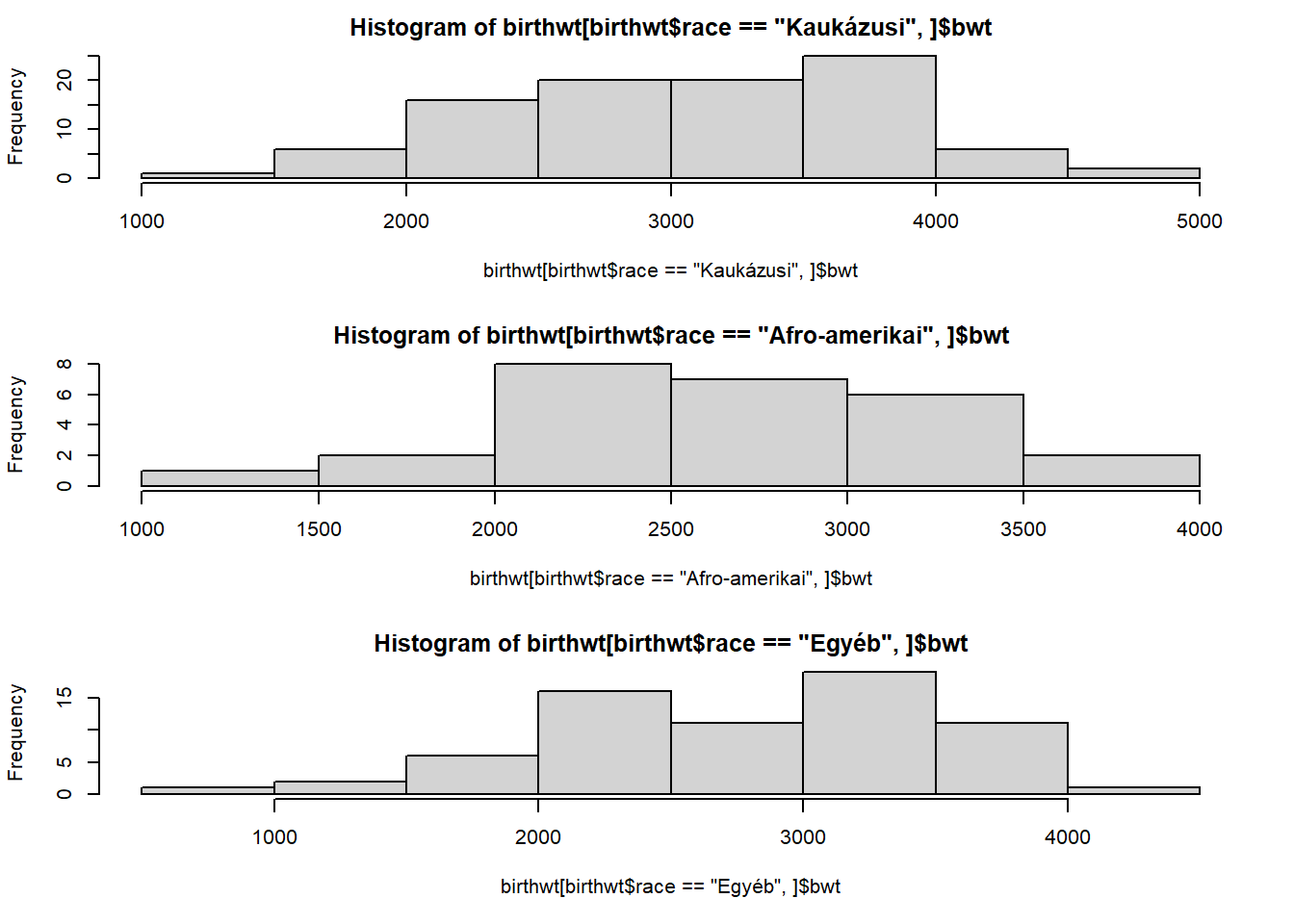
Figyeljük meg, hogy a dolog két szempontból is macerás: egyrészt nekünk, kézzel kell megoldani az adatbázis rászűrését a megfelelő rasszra, ráadásul még azt is nyomon kell követnünk3, hogy milyen rasszok vannak!
Egy apró technikai megjegyzés: ha már nincs szükségünk a felület szétosztására, akkor adjuk ki a dev.off() parancsot. Ez ugyanis nem csak törli a plottolási felületet, de egyúttal reset-eli a grafikus paramétereket, így az mfrow-t is.
A lényeg mindenesetre, hogy az ábra elkészült, és tudjuk használni!
…vagy mégsem? Túl azon, hogy nagyon rossz a helykihasználás a feleslegesen sok felirat miatt, még egy, elég nagy probléma van: nem ugyanaz a vízszintes tengelyek skálázása! Ami teljesen érthető is: az egyes hist hívások a többitől teljesen függetlenül futnak, így mindegyik a saját (egy rasszra leszűrt) adatbázisára fogja beállítani a vízszintes tengely határait! Ami igencsak nagy baj, hiszen mi az egész ábrát arra akarjuk használni, hogy a balra-jobbra eltolódásokat keressük, ehhez képest itt lehetetlen hogy legyen ilyen: még ha valamelyik rassz 1000 grammal nagyobb vagy kisebb is átlagosan, a fenti ábrán akkor is mindenki szép középen lesz… hiszen az hist így állítja be. És erre nem válasz az, hogy de ott van a vízszintes tengely beosztása, és azon ez látszik – az egész adatvizualizáció lényege, hogy segítsük az olvasót, az a lényeg, hogy minél egyértelműbben, minél automatikusabban, a legkevesebb „kognitív munkával” látszódjon az eredmény az ábrán. Ha számokat kell kiolvasni, több tengelyről, összehasonlítani, majd ez alapján elképzelni, hogy mi hol van, az már régen rossz. (Ezt az „elképzelést” kell nekünk, egy jó ábrával megvalósítani, az olvasó helyett, levéve róla ezt a terhet! Ekkor lesz az ábra igazán jó!)
Mi a megoldás? Természetesen az, hogy minden hisztogramot ugyanazzal a vízszintes tengelybeosztással kell kiplottolni. Igen ám, csakhogy ezt mi sem tudhatjuk, hogy mi! Azt kell megnézni, hogy mi a bwt teljes terjedelme, hogy mindegyik ábrán kiférjenek az adatok, és erre kell állítani az összes hisztogramot. De ezt mi sem tudhatjuk, hogy mennyi, ezért először kérdezzük le kézzel:
range(birthwt$bwt)[1] 709 4990Ezt némileg kerekítve most már elkészíthetjük a jó ábrát, természetesen minden egyes hisztogramnál kézzel beállítva ezeket a határokat:
par(mfrow = c(3, 1))
par(mar = c(5.1, 4.1, 2.1, 2.1))
hist(birthwt[birthwt$race == "Kaukázusi",]$bwt, xlim = c(500, 5000))
hist(birthwt[birthwt$race == "Afro-amerikai",]$bwt, xlim = c(500, 5000))
hist(birthwt[birthwt$race == "Egyéb",]$bwt, xlim = c(500, 5000))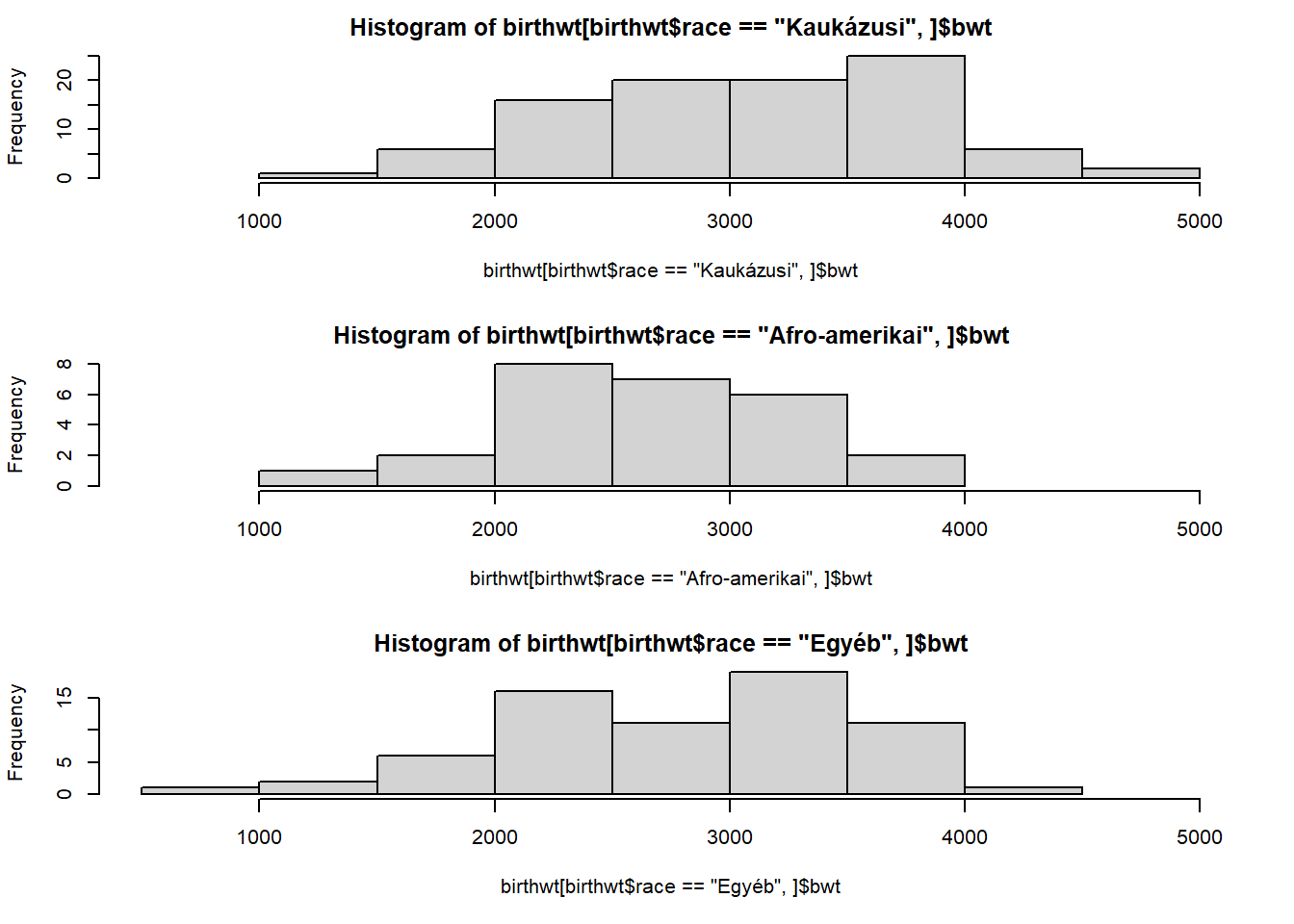
Sikerült létrehozni az ábrát? Igen. Egyszerű volt a dolog? Nem. Meg tudtuk oldani, de oda kellett figyelni, rengeteg dolgot kézzel kellett állítani, mindegyik ilyen kivétel nélkül hibalehetőség, a maceráról nem beszélve. És még így is egy olyan ábra jött létre ami… khm, komoly vizuális kihívásokkal terhelt.
Talán ennél is nagyobb problémákra mutat rá a következő példa. A feladat legyen ugyanez, annyi módosítással, hogy most nem hisztogramot, hanem magfüggvényes sűrűségbecslőt akarunk alkalmazni az egyes eloszlások vizualizálására.
A magfüggvényes sűrűségbecslő előnye, hogy ilyenből több is ráplottolható ugyanarra az ábrára (nyilván valamilyen módon, például színnel megkülönböztetve ezeket), ami azért előnyös, mert jobban összehasonlíthatóak azok a dolgok, amik ugyanazon az ábrán vannak.
Álljunk neki a feladatnak! Az egyetlen dolog, amire figyelni kell, hogy az első KDE-t ábrázolhatjuk plot-tal, de a másodikat már nem, mert a plot mindig elsőként letörli a plottolási felületet. De semmi gond nincs: a density objektumot átadhatjuk egy lines-nak is, ami pont ezt a problémát oldja meg, mert ugyanazt csinálja mint a plot, de nem üríti a felületet, hanem a meglevőre ráplottol – pont amire szükségünk van! Nézzük is; természetesen a színt nekünk kell, kézzel beállítanunk:
plot(density(birthwt[birthwt$race == "Kaukázusi",]$bwt))
lines(density(birthwt[birthwt$race == "Afro-amerikai",]$bwt), col = "blue")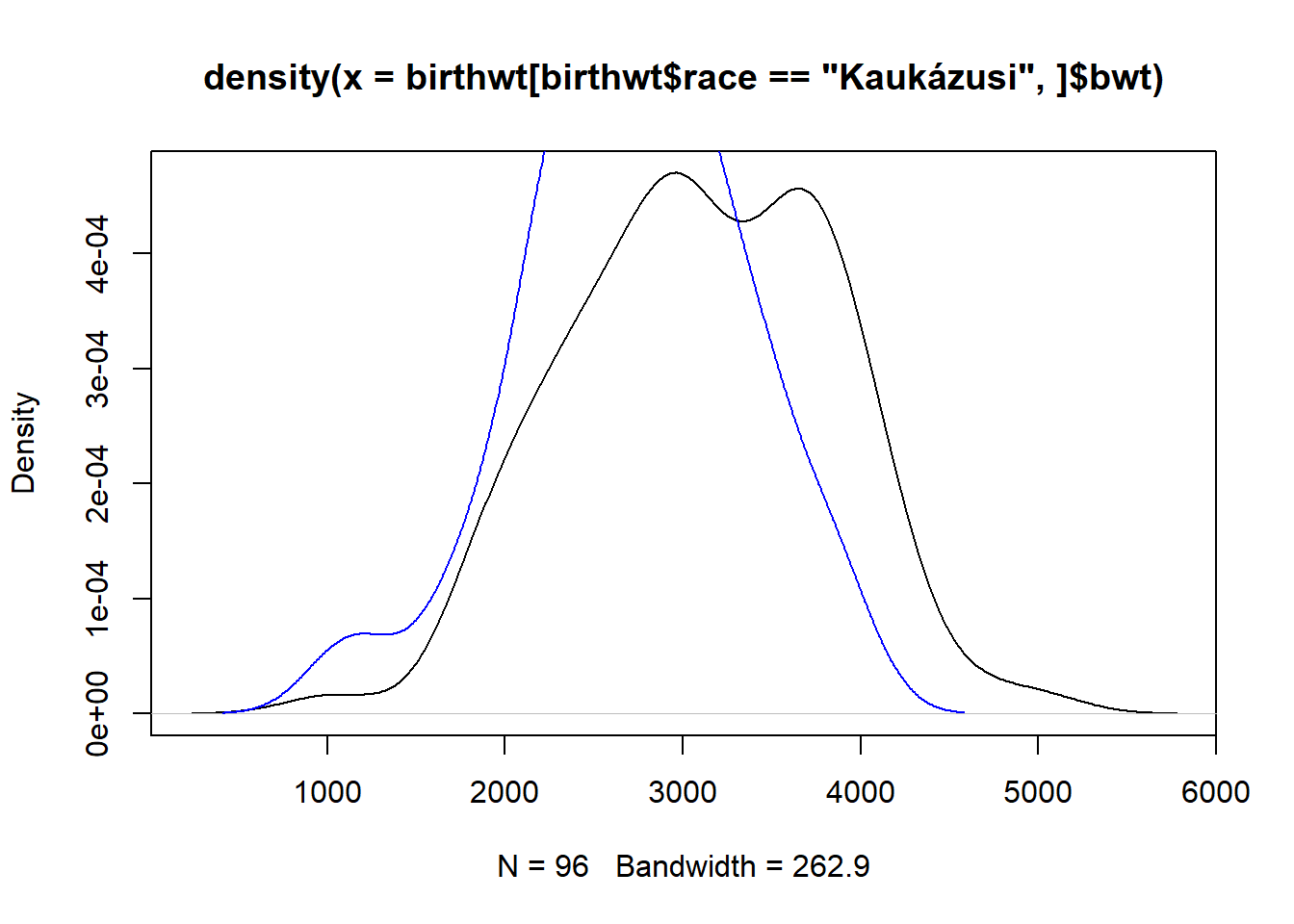
Baj van: a második görbe kifut az ábra tetején. De ha végiggondoljuk, hogy mi történt, akkor nagyon hamar rájövünk, hogy mi a probléma forrása: az ábra koordinátatengelyeit az első hívás állította be – természetesen az ott használt, kaukázusira leszűrt adatbázis alapján! A lines ráplottol, vagyis természetesen nem tudja, visszamenőleg, megváltoztatni a függőleges tengely határait…!
Próbáljunk a dolgon javítani. A megoldás nem bonyolult: egyszerűen meg kell növelni a függőleges tengely tartományát. (Természetesen kézzel beállítva!) Itt azonban van egy plusz-probléma: nem nyilvánvaló, hogy mire kell állítanunk. Az előző példánál is volt hasonló probléma, csak ott legalább ez a gond nem volt, mert a range használatával egyszerűen lekértük, hogy mik a határok. De a függőleges tengelyre, tehát, hogy a sűrűség meddig fut fel, nincsen range, ezt nem tudjuk sehogy lekérdezni, vagy megtudni…! Mondhatnánk, hogy akkor először plottoljuk a második rasszt (hiszen az úgy beállított tengelyekre az első már biztosan ráfér), de ez sem oldja meg a problémát, mert mi van, ha a harmadik még nagyobb? Voltaképp arról van szó, hogy a kísérletezést sehogy nem tudjuk megspórolni, akkor kísérletezzünk (próbálgatásos alapon – hiszen jobb eszközünk nincs!) inkább a függőleges tengely skálázásával:
plot(density(birthwt[birthwt$race == "Kaukázusi",]$bwt), ylim = c(0, 5e-04))
lines(density(birthwt[birthwt$race == "Afro-amerikai",]$bwt), col = "blue")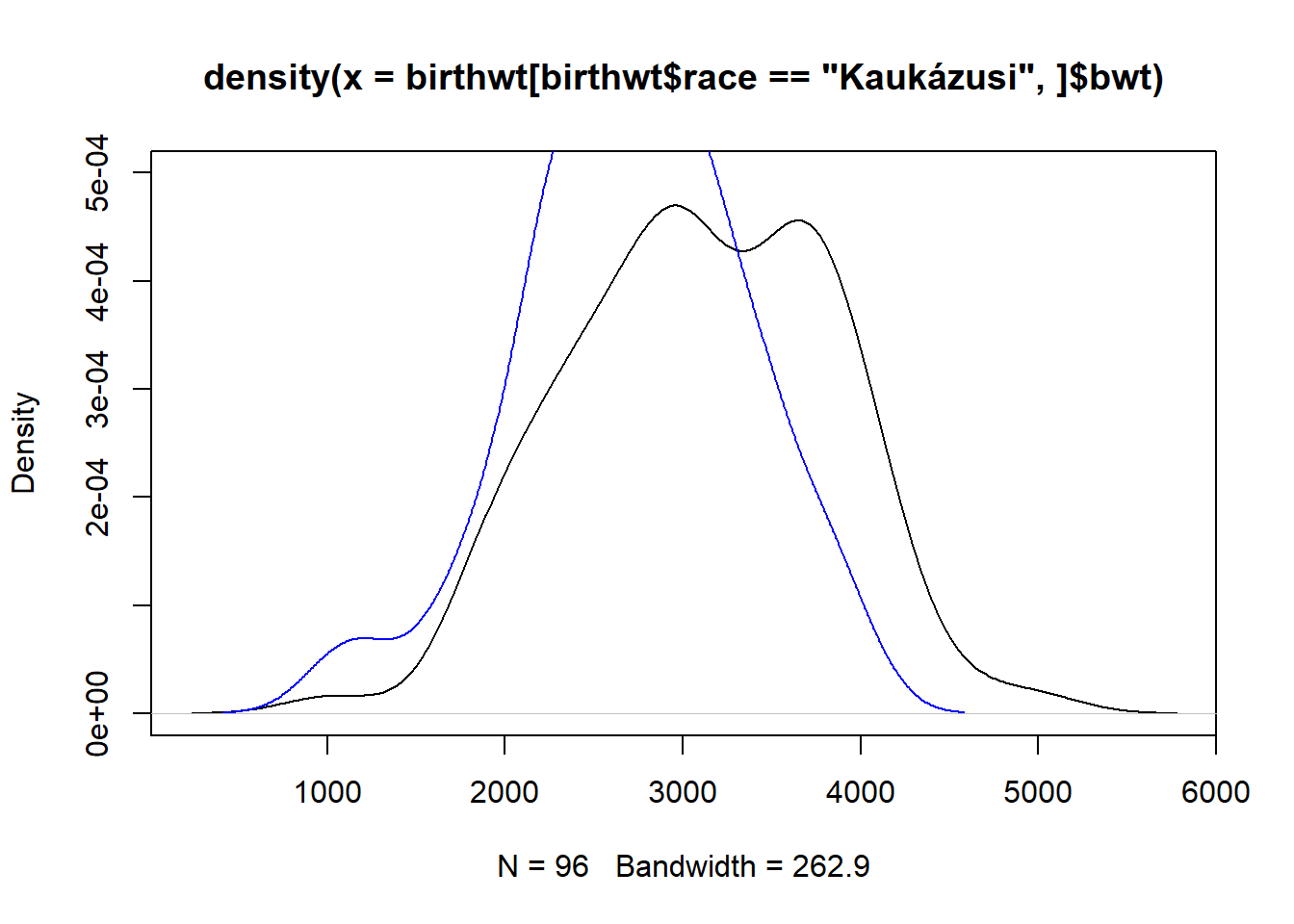
Sajnos nem jó a dolog, ez a felső határ nem elég. Próbáljuk újra:
plot(density(birthwt[birthwt$race == "Kaukázusi",]$bwt), ylim = c(0, 5e-03))
lines(density(birthwt[birthwt$race == "Afro-amerikai",]$bwt), col = "blue")
Na, ezzel meg túllőttünk a célon – belefér minden ugyan, de nagyon kicsire vannak összenyomva, nem használjuk ki a területet, ami szintén nem jó. Próbáljuk még egyszer:
plot(density(birthwt[birthwt$race == "Kaukázusi",]$bwt), ylim = c(0, 6e-04))
lines(density(birthwt[birthwt$race == "Afro-amerikai",]$bwt), col = "blue")
lines(density(birthwt[birthwt$race == "Egyéb",]$bwt), col = "red")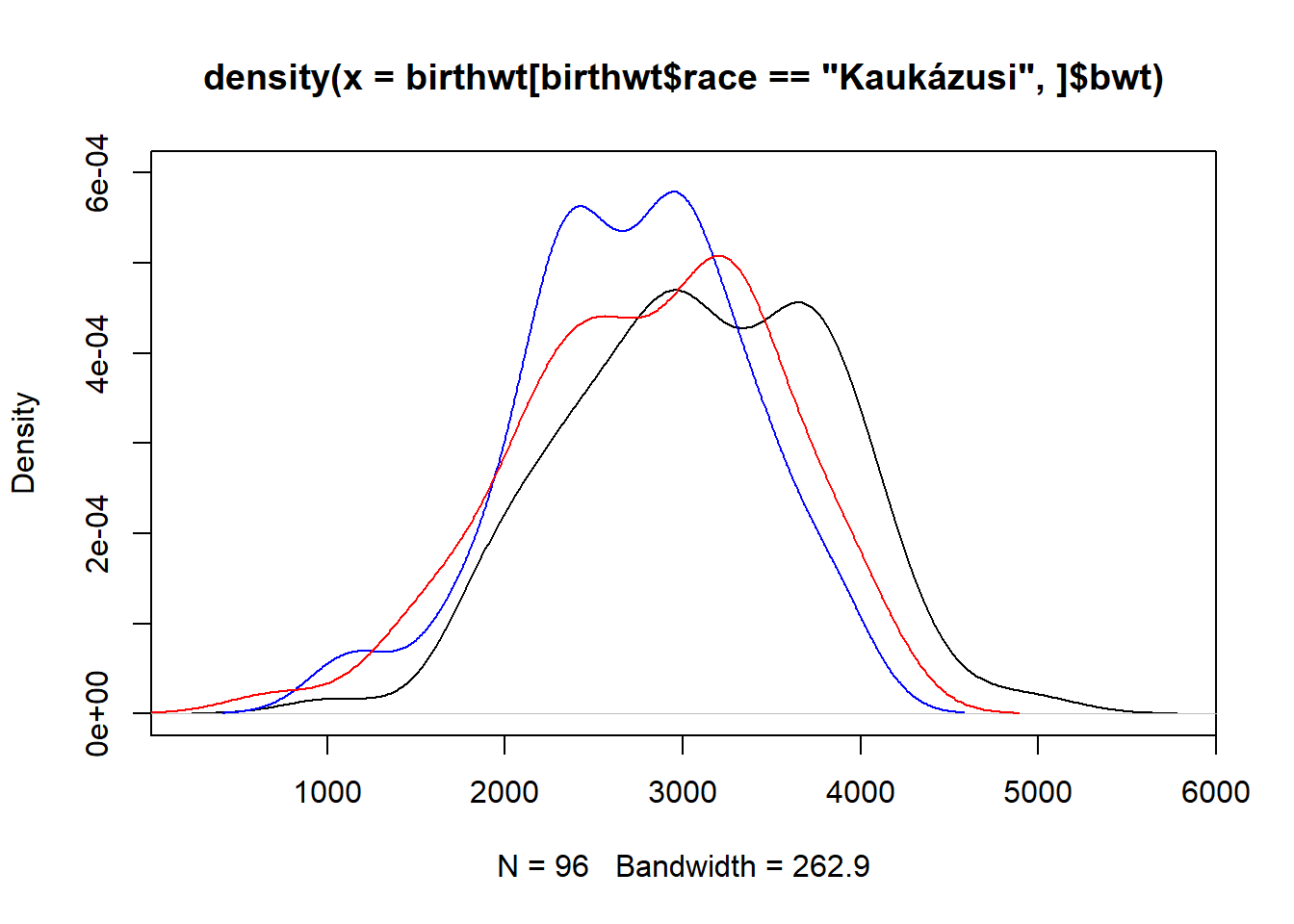
Most már stimmel!
Illetve… egy apró, de azért meglehetősen kézenfekvő probléma még mindig van: melyik szín mit jelent?? Na igen, ugyanis nincsen jelmagyarázat, e nélkül nem sokra megyünk az ábrával… Szerencsére a base R grafikának van jelmagyarázatot készítő függvénye, az a neve, hogy legend, át kell neki adni a jelmagyarázat pozícióját, valamint a feltüntett szövegeket és színeket:
plot(density(birthwt[birthwt$race == "Kaukázusi",]$bwt), ylim = c(0, 6e-04))
lines(density(birthwt[birthwt$race == "Afro-amerikai",]$bwt), col = "blue")
lines(density(birthwt[birthwt$race == "Egyéb",]$bwt), col = "red")
legend("topleft", c("Kaukázusi", "Afro-amerikai", "Egyéb"),
fill = c("black", "red", "blue"))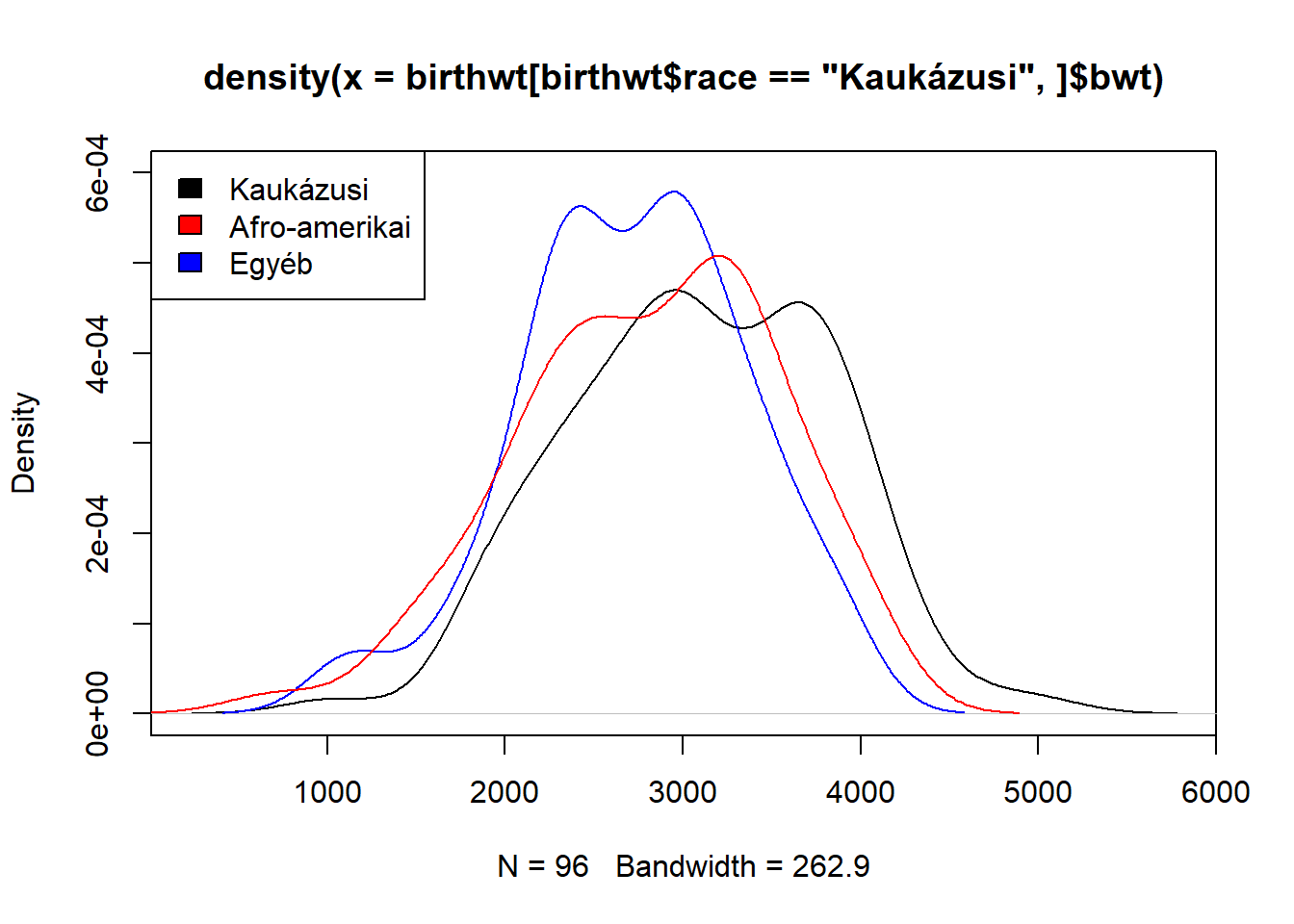
Most már minden tökéletes! Ugye?
…vagy mégsem?
Aki szerint minden tökéletes, nézze meg még egyszer, jobban a színeket…
A harci helyzet ugyanis az, hogy elrontottam a jelmagyarázatot. Igen, elrontottam, ugyanis semmi nem kapcsolja össze, hogy a jelmagyarázatban mi jelenik meg, és hogy az ábrán mi van…! Következésképp simán meg lehet tenni, hogy a jelmagyarázatban mást tüntetünk fel, mint ahogy az ábra készült! E felett semmiféle kontroll, ellenőrzés, figyelmeztetés nincs; egyetlen pillatnyi figyelmetlenség a mi részünkről, és teljesen rossz ábra készül! (Ha ráadásul az R kódot nem adjuk meg, csak az ábrát, ez soha ki sem derül…!)
Remélem ez a példa végképp demonstrálta, hogy az ilyen ábrák összerakása base R grafikával, még ha lehetséges is, nagyon macerás, és, ami még nagyobb baj, hatalmas hibalehetőségeket rejt magában. Szoktam mondani, hogy ha egy ábrára legend kell vagy több részábrából áll, az jó jel arra nézve, hogy elgondolkozzunk, hogy inkább ne base R grafikában valósítsuk meg.
De akkor miben?
4.2 Haladó adatvizualizációs csomagok, a ggplot2
Az elmúlt évtizedek alatt nagyon komoly munka folyt olyan haladó adatvizualizációs csomagok kialakítására, melyek lehetővé teszik a komplex, adott esetben nagyon komplex tudományos adatvizualiciók relatíve egyszerű, hibaálló, jól átlátható kóddal történő elkészítését R alatt. Azért fogalmaztam úgy, hogy „relatíve”, mert az ilyen megoldások a legegyszerűbb feladatokra tipikusan bonyolultabbak, mint a base R grafika – de cserében a bonyolultabbakra jobban működnek, vagy egyáltalán, működnek.
A mai napra két csomag kristályosodott ki, amelyeket a fenti célra széleskörűen használnak. Az egyik az eredetileg Deepayan Sarkar által kifejlesztett lattice, a másik az eredetileg Hadley Wickham által kifejlesztett, de ma már egy komoly csapat által karbantartott ggplot2. Adja magát a kérdés, hogy melyik a jobb (melyiket érdemes megtanulni?), de erre nem könnyű válaszolni. Eleve, mi az, hogy „jobb” egy ilyen esetben…? Ennek egy sor szubjektív komponense van, így a kettő közti választás helyenként kissé hitvita jellegű, de ami objektív, az a népszerűségük: erre több metrika elérhető, például, hogy mennyien töltik le az egyes csomagokat a CRAN-ról, vagy, hogy hány kérdést posztolnak a csomagokról a Stackoverflow-n. Nézzük most meg az előbbit az erre a célra jól használható cranlogs csomag segítségével! Így alakult a két csomag letöltéseinek a száma 2024 évben:
data.table::data.table(cranlogs::cran_downloads(
c("ggplot2", "lattice"), from = "2024-01-01", to = "2024-12-31"))[
, .(count = sum(count)), .(package)] package count
<char> <num>
1: ggplot2 22145132
2: lattice 1253856Amint látható, a ggplot2 nagyságrendileg múlja felül a lattice csomagot. Anélkül, hogy a hitvita részében különösebben állást foglalnék, most a ggplot2 csomagot fogom bemutatni.
4.2.1 A ggplot2 alapjai: ggplot, geom és aes
A ggplot2 a nevét egy könyvről kapta: Leland Wilkinson amerikai statisztikus 1999-ben adta ki a Grammar of Graphics, azaz a „Grafika nyelvtana” című művét. A könyv a korszakban elég formabontó volt; mint neve is mutatja, egyfajta nyelvtant akart a grafika mögé tenni: olyan rendszert, melyben az ábrák strukturáltan (adott nyelvi elemek kötött módon történő kombinálásával) írhatóak le. Hadley Wickham úgy indította el az R csomagját 2006-ban, mint ami megvalósítja az e könyvben leírt gondolatokat, egyfajta implementációja Wilkinson elméleti keretrendszerének. (Azzal, hogy ezt a keretrendszert kicsit maga is módosította a csomag céljaira, nem szó szerinti átvétele Wilkinson gondolatainak.) A nyelvtan léte egy adatvizualizációs rendszerben egyszerre nehézség, hiszen egy adott struktúrához alkalmazkodás megköti az ember kezét, és hatalmas erő, mivel lehetővé teszi még a bonyolult feladatoknak is az egységes4, szisztematikus megközelítését, megoldását. A csomag elég hamar átesett egy teljes átalakításon5, ami után ráadásul az új verzió egyáltalán nem volt kompatibilis a régivel, ezért egy új csomagba tette ezt – ez lett a ggplot2.
A ggplot2 felfogása, az előbb említett nyelvtanból fakadóan nagyban eltér a base R grafikától, ezért nem triviális az áttérés, igényel némi beleszokást, amíg az ember agya átáll a ggplot2 logikájára6 – a dolog azonban, mint már láttuk is, bármilyen kicsit is komolyabb vizualizációs feladatnál megtérül (illetve elkerülhetetlen). A ggplot2-re egyszerre igaz az, hogy nagyon jó alapbeállításai vannak, melyekkel gyakorlatilag azonnal „publication quality” ábrákat készíthetünk minden további beállítás nélkül, de közben az is igaz, hogy ha szeretnénk, akkor a legapróbb részletekig testreszabhatjuk az elkészített ábrákat.
Elsőként töltsük be7 a ggplot2 csomagot (ezt általában nyugodtan megtehetjük, hiszen sok esetben ez egy alapvetően és gyakran használt csomag egy szkriptben, így védhető a library-vel történő betöltés):
library(ggplot2)Egy ggplot2 grafikának három kritikus komponense van:
- Az adatok (melyeket leírnak az adatváltozók). Mi most tudományos adatvizualizációkról beszélünk, így az ábráink tartalma valamilyen adatokon alapszik. Ezeket az adatokat egy (ritkábban több) adatbázisban – tipikusan adatkeretben, vagy valamilyen azzá átalakítható objektumban – tároljuk, és megadjuk az ábrázolási utasításnak, „betápláljuk” őket az ábrába. Ilyen értelemben amit úgy hívtam, hogy adatváltozó, az nem más, mint egyszerűen az adatforrás oszlopa (hiszen egy adatkeret változói az oszlopai).
- A grafikus elemek (melyeket leírnak a grafikus változók). Az ábra „tényleges tartalma”, a rajta megjelenített grafikos objektumok, legyen az akár egyetlen pont, akár egy komplett hisztogram. A
ggplot2ezeketgeom-nak hívja (például a pont ageom_point, a hisztogram ageom_histogram). Ezeknek az objektumoknak mind vannak – megjelenésüket szabályozó – paramétereik, ezeket hívtam az előbb grafikus változónak; például egy pontnál ilyen az \(x\) és \(y\) koordinátája, vagy épp a színe. Ageom-ok súgója, például?geom_pointerről az „Aesthetics” pont alatt ad felvilágosítást, ahol valamennyi grafikus változó szerepel. A kötelezőek vastagon vannak szedve, például egy pontnál kötelező, hogy megadjuk a két koordinátáját, de nem kötelező, hogy gondoskodjunk szín beállításáraól (mert annak van alapértelmezett értéke). - A grafikus és adatváltozók közötti leképezés. Ez az utolsó pont: össze kell kötni egymással a grafikus és adatváltozókat, meg kell adni, hogy adott grafikus változónak mely adatváltozó felel meg, azaz adott grafikus változó mely adatváltozóból kapja a tartalmát. Például azt mondjuk, hogy
x = lwt, ez majd azt fogja jelenteni, hogy ageom-nak azxnevű változója az adatbázisunklwtnevű oszlopából nyerje az értékét (egygeom_pointesetén: a pont \(x\) koordinátája azlwtértéke legyen). Aggplot2ezt úgy hívja, hogy „aesthetic mapping”. Ezt megadni azaesnevű függvénnyel lehet, úgy, hogy argumentumokként, tehát vesszővel elválasztva, megadjuk az összerendeléseket: minden összerendelésben van egy egyenlőségjel, bal oldalán a grafikus változó, jobb oldalán az adatváltozó. Például:aes(x = lwt, y = bwt).
A fenti lényegében egy recept: rajzolj ki adott geom-okat, ehhez persze tudni kell bizonyos dolgokat (mondjuk egy pontnál a koordinátáit), ezt megkapod az aesthetic mapping-ből, ami megadja, hogy ezeket milyen nevű változóban kell keresned, és tessék, itt van hozzá a konkrét adatbázis, ahol megtalálod ezeket a változókat!
Egy ggplot2 hívás mindig a ggplot függvény meghívásával kezdődik. Általában rögtön megadjuk a felhasznált adatbázist is (első argumentumként) és az esztétikai leképezést (második argumentumként). Ezek nem kötelezőek – elvileg a ggplot() is egy tökéletesen értelmes hívás, és szükség is lehet rá, de inkább csak a komplexebb ábráknál, úgyhogy erről majd később. A példa kedvéért tételezzük fel, hogy egy szóródási diagramot akarunk készíteni a már látott adatbázisunk bwt és lwt változóiról! Azonosítsuk a komponenseket: milyen grafikus objektumra van szükségünk? Pontokra, úgyhogy ez geom_point-ot igényel. Mi az adatbázisunk? A birthwt. Mi az esztétikai leképezés? Az x értékét összekötjük az lwt-vel, az y-t a bwt-vel. Ez alapján kezdjük is el! Ahogy már utaltam rá, egyszerűbb esetekben a ggplot meghívásában rögtön megadjuk az adatbázist és a leképezést:
ggplot(birthwt, aes(x = lwt, y = bwt))
Amint látható, ez nem rajzol ki semmit – érthető módon, hiszen nem is szerepel benne semmilyen geom. És ezen a ponton eljutunk a ggplot2 következő, rendkívül fontos jellemzőjéhez.
A ggplot2-ben az ábrákat nem egyetlen függvény meghívásával alakítjuk ki, hanem sok kis függvényhívásból, mint apró építőelemekből rakjuk össze. A „rakjuk össze” kifejezés nem volt teljesen véletlen: ezeket a függvényhívásokat + jellel kell egymás után írni a ggplot2-ben. Erről a szintaktikáról később még sokat fogunk beszélni, egyelőre annyi a fontos, hogy úgy kell elképzelnünk, hogy a ggplot2 végigolvassa az egész sort, egymás után mindent amiket felsoroltunk + jellel, majd mindegyiket felhasználva összerakja az ábrát.
A + szintaktika annyira erős, hogy még a geom-okat is így kell megadni. A fenti esetben:
ggplot(birthwt, aes(x = lwt, y = bwt)) + geom_point()
És ezzel meg is vagyunk – elkészült az első teljes értékű ggplot2 grafikánk!
E ponton valaki azt mondhatja, hogy ez a sok hűhő semmiért esete, sőt, még rosszabb is, feleslegesen bonyolítottuk az életet, mikor ugyanezt egy plot(bwt ~ lwt, data = birthtwt) hívással el lehetett volna intézni8. Az egyik kérdés az esztétika: sokan mondják, hogy a ggplot2-vel szebb ábrát kaptunk. Ez persze némileg szubjektív. Van itt azonban még valami.
Tételezzük fel, hogy egy kicsit kibővítjük a feladatot: készítsük el a szóródási diagramot… de úgy, hogy a pontokat a rassz szerint beszínezzük! (Miért tennénk ilyet? Erre még visszatérünk, de most gondoljunk rá úgy, mint egyfajta háromváltozós vizsgálatra! Ahol két változó mennyiségi, egy pedig minőségi.) Mielőtt bármit csinálunk ggplot2-ben, egy pillanatra képzeljük el, hogy ez hogyan nézne ki base R grafikában! Végig kellene menni a rasszokon, mindegyiket kiplottolni, közben persze kibukik, hogy ha az első véletlenül nem a legnagyobb terjedelmű (immár ráadásul két tengely mentén), akkor a tengelyek skálázása rossz lesz, úgyhogy ezt be kell állítanunk, és ha ez mind megvan, jövünk rá, hogy hoppá, de nincs is jelmagyarázat, amit rakhatunk rá, de csak kézzel beállítva a tartalmát…
Na de mi a helyzet ggplot2 alatt? Nézzük végig a komponenseket! Változott az adatforrás? Nem. Változott, hogy mi vagy mik a megjelenített grafikus elemek? Nem. (Attól még mert be van színezve, azok ugyanúgy pontok.) Mi az egyetlen dolog ami változott? Az esztétikai leképezés! A pontnak ugyanis van egy szín nevű grafikus változója, csak eddig nem használtuk – megtehettük, mert van alapértelmezése, ezért lett minden fekete. De ez alapján azt gondolhatjuk, logikusan, hogy nincs más dolgunk mint most azt is beállítani, vagyis, hozzárendelni egy adatváltozóhoz. Tehát akkor elég lenne egy color = race hozzáadása…? Próbáljuk ki:
ggplot(birthwt, aes(x = lwt, y = bwt, color = race)) + geom_point()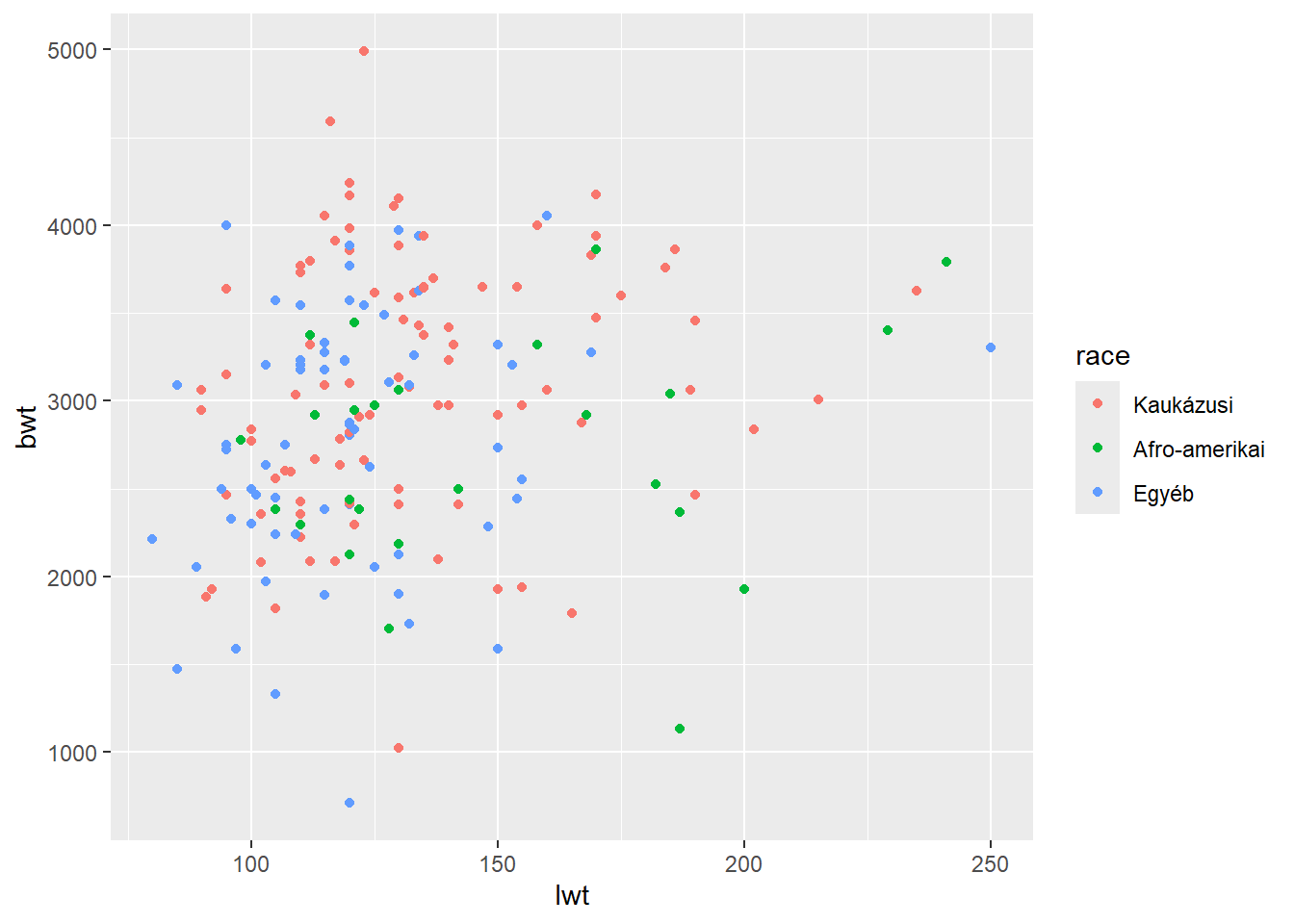
Igen! A megoldás tökéletesen működik.
Megint gondoljunk egy pillanatra vissza arra, hogy ez milyen lett volna base R grafikában; de ha valakit még ezzel sem sikerült elrettentenem, akkor bővítsük még egy nagyon kicsit a feladatot: rajzoljunk egy szóródási diagramot, színezve rassz szerint, és kétféle különböző alakú jelölővel az alapján, hogy az anya dohányzik-e! Most már minden kommentár nélkül a megoldás (annyit kell tudnunk, hogy az alak micsoda, nem nehéz kitalálni sem, de a ?geom_point természetesen megadja):
ggplot(birthwt, aes(x = lwt, y = bwt, color = race, shape = smoke)) +
geom_point()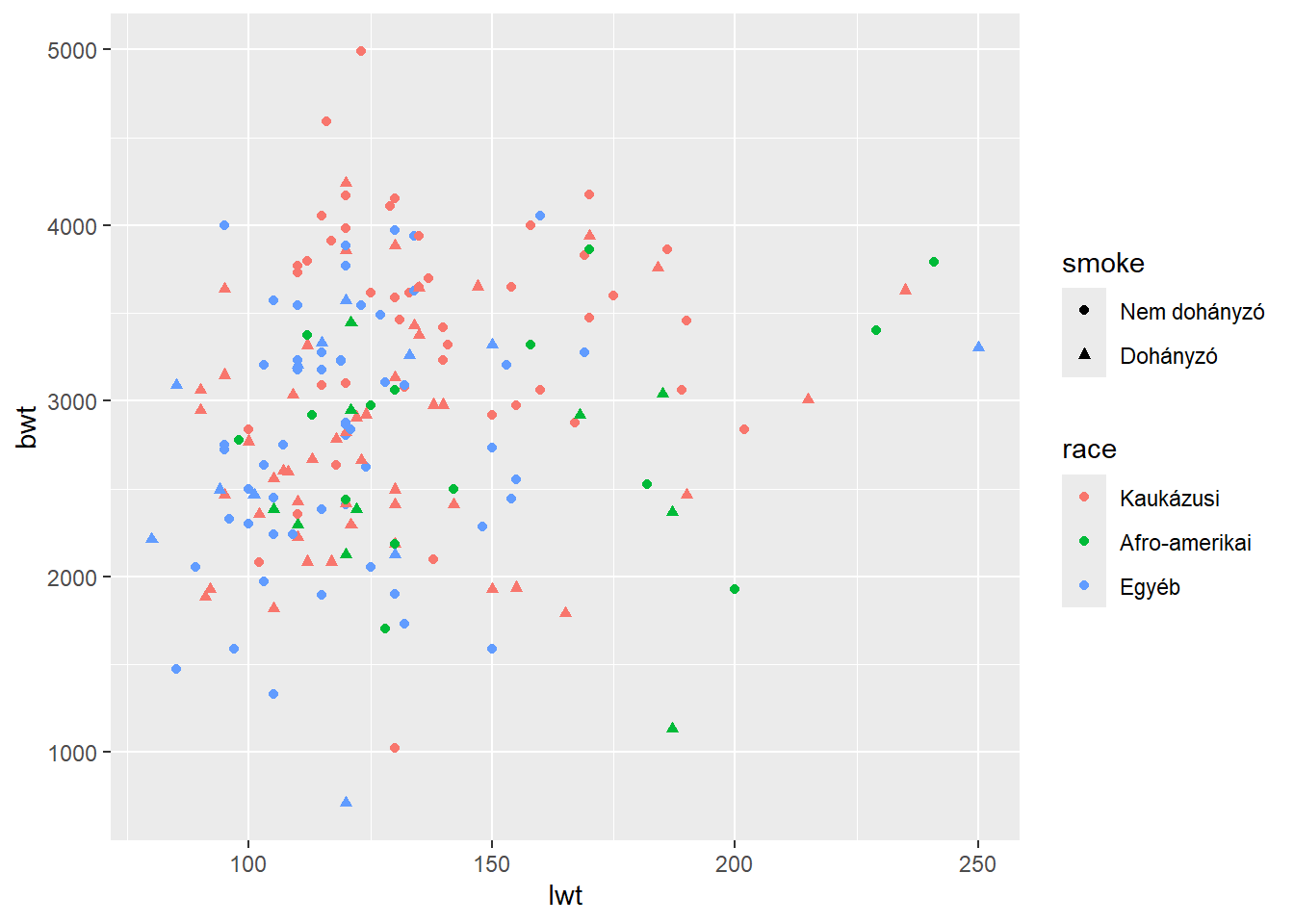
Itt már nem is említem, hogy ennek az összerakása hogyan nézne ki base R grafikában… ggplot2 alatt pedig egyetlen kódsor!
4.2.2 A + jeles szintaktika
Az előbbiekben azt mondtam, hogy a + jel használata nagyon felületesen nézve olyan, mint a base R grafikában a „ráplottolás” – újabb és újabb dolgokkal egészíthetjük ki az ábrát. (Még a geom-ból is nyugodtan használhatunk többet az össze-+-ozott dolgok között.) Van azonban egy hatalmas különbség.
A dolgot egy meglehetősen banális példán mutatom be: szeretnénk a szóródási diagramunkra szép, értelmes tengelyfeliratokat tenni. Az általános szabály itt is működik: míg base R grafikában ezeket (is) argumentummal állítottuk be, a ggplot2-ben ezeket (is) +-olni kell. Igen, ugyanis van erre egy külön ggplot2-es függvény, és igen, azt is + jellel kell hozzáadni:
ggplot(birthwt, aes(x = lwt, y = bwt)) + geom_point() +
labs(x = "Anyai testtömeg [font]", y = "Születési tömeg [gramm]")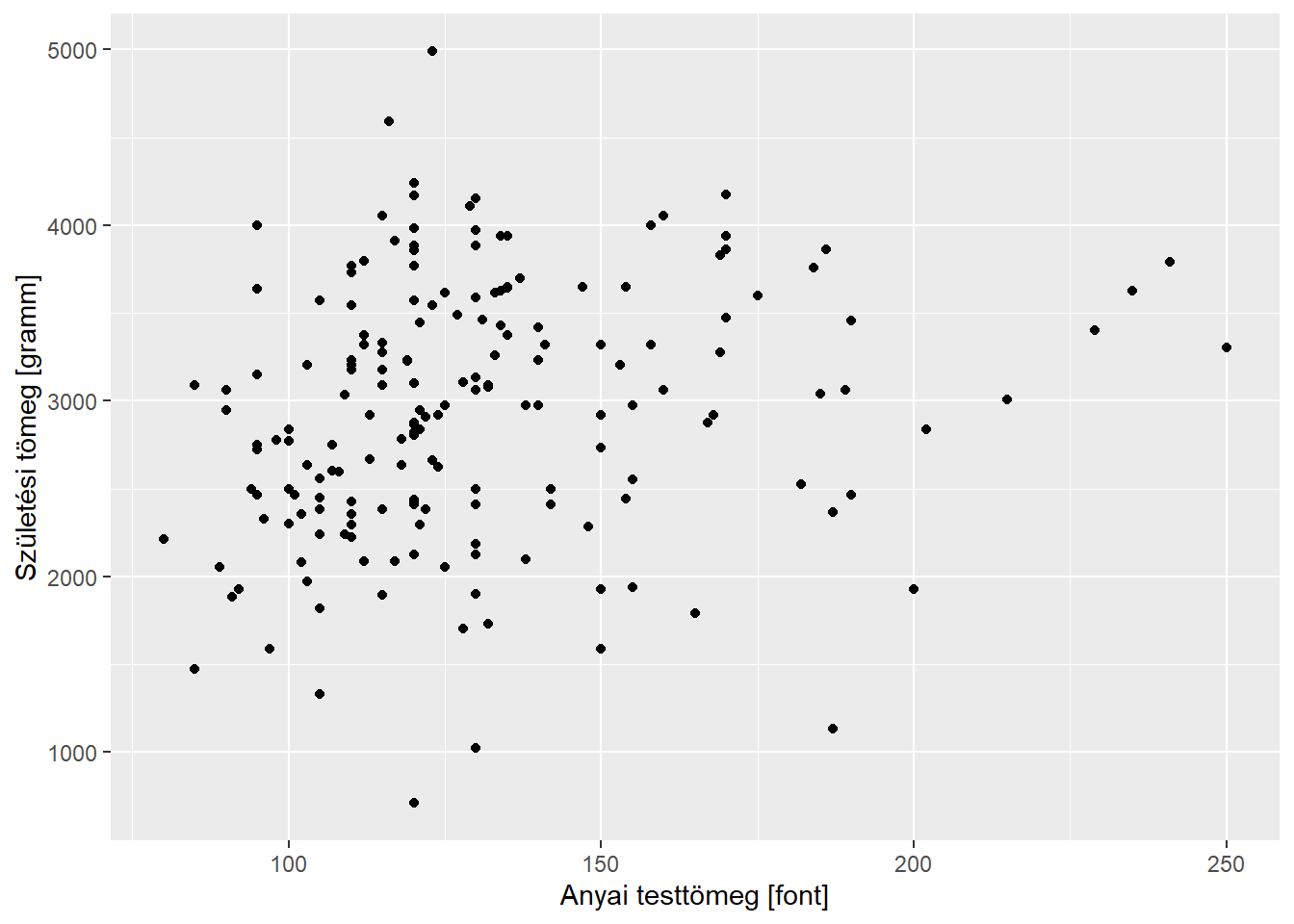
Ha azonban jobban megfigyeljük ezt az ábrát (illetve összevetjük a korábbival), akkor hamar felfedezhetünk egy nagyon fontos dolgot: ez nem pusztán ráplottolás volt! Hiszen ha megnézzük a tengelyfeliratokat, akkor láthatjuk, hogy nem csak megjelent az új – de eltűnt a régi! Magyarán: szemben a base R grafikás ráplottolással, a + jeles szintaktikának lehet visszaható hatása is: valaminek a rá-+-olása nem csak hozzáadhat új dolgokat, hanem megváltoztathat olyat is, ami már rajta volt az ábrán. Ez élesen szemben áll a base R grafikás ráplottolással, ahol ilyen nem történhet meg.
A magyarázat természetesen az, hogy a ggplot2 a + jelekből felépített hívást egészében értelmezi. Ilyen módon a + jeles szintaktika valójában nem a ráplottolásról szól, hanem egyfajta eszköz: a filozófia az, hogy a komplex ábrát sok apró építőelemből rakjuk össze, ilyen építőelemből többet alkalmazva, azokat egymással kombinálva. Ez a megközelítés azért működik jól, mert ha egyetlen hívásba kellene mindent belezsúfolnunk, az nagyon hamar kezelhetetlen és áttekinthetetlen lenne, viszont ezzel a fajta építkezéssel egész komplex ábrák is felépíthetőek követhető, kézbentartható módon. Itt kell kiemelni a dolog iteratív jellegét (amit ez a filozófia kiválóan támogat): a ggplot2-ban sokszor úgy rakunk össze komplex ábrát, hogy indulunk egy egyszerűből, és folyamatosan bővítjük, míg el nem jutunk a szükséges végeredményhez. Ez nem csak didaktikus, és így a tanulást segítő, de a tényleges munkát is nagyban könnyíti.
Beépített, azaz külön csomag betöltése nélkül is elérhető. Valójában ezek a függvények is valamilyen csomagban vannak – jellemzően a
graphics-ban – csak ezek a csomagok automatikusan betöltődnek az R indulásakor.↩︎A
marparaméter beállítására tisztán technikai okokból van szükség. Ez az ábra körüli margók szélességét adja meg base R grafikában; kicsit le kell csökkenteni, hogy kiférjen az oldalon.↩︎Ez utóbbin lehetne segíteni egy
for-ciklussal – itt most joggal használnánkfor-ciklust, ahistegy mellékhatásos függvény – ami ezt a problémát megoldaná, de behozná afor-ciklust, mint plusz programozási eszközt; úgyhogy most maradtam az egyszerű, kézi megvalósításnál.↩︎Ahogy a
ggplot2szerzői egy helyen fogalmaznak: nyelvtan nélkül egy adatvizualizációs csomag nem más, mint „speciális esetek hatalmas gyűjteménye”.↩︎Az eredeti
ggplot-ban még nem volt meg a+jeles szintaktika, hanem mindent függvények egymásba ágyazásával oldott meg – csak úgy, mint az R nyelv maga! Lényegében tehát aggplot2újítása ugyanaz filozofikusan, mint ami a pipe operátor az R-ben – csak épp évekkel amagrittrcsomag, és pláne a beépített pipe előtt. Ha valakit érdekel, az eredetiggplot(néha megkülönböztető néven:ggplot1) kódja megtalálható az interneten.↩︎A
latticeezzel szemben sokkal direktebb kiterjesztése a base R grafikának, nem igényel teljes átállást egy szinte komplettül más alapokra építkező logikára.↩︎A
ggplot2nem jön az alapértelmezett R letöltéssel, ezértinstall.packages("ggplot2")-vel, vagy RStudio alatt a Tools / Install packages-zel előbb telepíteni kell.↩︎A
ggplot2-ben van egyqplotnevű függvény, pont az ilyen esetekre: a nagyon egyszerű hívások összerakhatóak vele, egyszerűbb szintaktikával. A használatát nem javaslom: a legegyszerűbb eseteken kívül semmit nem nyerünk vele, közben zavaró lehet a szintaktikai kettősség, ráadásul aggplot2tanulását is nehezíti – jobb ha az ember eleve is a teljes körű, minden eset megoldására alkalmas szintaktikát tanulja meg, ehhez igazán nem nagy ár ez a néhány plusz utasítás az ilyen legegyszerűbb esetekben. Úgy tűnik aggplot2fejlesztői is hasonlóan gondolkodnak, mert a 3.4.0-s verzióban „deprecated” állapotúra rakták ezt a függvényt.↩︎